ROKO
Ensemble (Bagging, Boosting) 본문
Ensemble (앙상블)
- Combine multiple models into a ensemble
- Better than the individual model
- Particularly well suited to decision trees in ML
- Intution : majority is less likely to make mistakes and has more information than individuals
How to make different models with same structure?
앙상블은 여러 모델을 혼합하여 하나의 모델로 구성하는데 한 종류의 모델을 가지고 앙상블을 구성하기 위해서는 각 모델들이 구조는 같을 지라도 서로 다른 모델로 구분되어야한다. 이를 위해 아래와 같은 방식을 적용해 볼 수 있다.
- Different algorithm
- Different choices of hyperparameters
- Trained on different data
- Trained with different weighting of the training examples
기본적으로 앙상블은 Loss 값 식을 데이터의 편향과 분산의 합으로 분해하여 둘중 값을 줄이는 식으로 구현한다.
We need to understand concepts of generalization using the bias/variance decomposition
Loss Function
A loss function L(y, t) defines how bad it is about prediction
Example : 0-1 loss, squared error loss, Mean squared error(MSE), Mean absolute error(MAE)

Loss funcition을 어떻게 bais/variance decomposition을 이용해 해석 할 수 있을까?
x에 대한 예측은 예측값 확률변수 y에 의해 결정된다. 그렇다면 y는 어떻게 구해지는 걸까?

P data에서 Train set과 Test set 을 구분하여 분할한다. 이때 Train set을 가지고 학습한 가설 h가 Test set의 데이터 x를 예측한 결과값 y와 실제 label t와 비교하여 Loss값을 구한다. 그렇게 모든 Test data들에 대한 평균 Loss\(E(L, t) | x)\)를 통해 정확률을 계산한다. 중요한 포인트는 Train set과 Test set은 서로 다른 데이터로 독립이라는 것이다.
Bias-Variance Decomposition: Baisc Setup
- Data generating distribution 에서 추출된 훈련데이터셋 \(D\)는 \((x_{i},t_{i})\) 형태로 구성되어 있고 독립이며 같은 확률 분포를 가지고 있다. (iid, independent and identically distrubuted)
- Fix Query point (예측하고자 하는 데이터를 고정)
- 독립적으로 추출된 많은 훈련데이터셋에 대해 실험을 고려한다.



위의 그래프는 분류, 회귀에 대해 학습을 진행했을때 Query point x에 대한 예측값 y에 대한 결과를 나타낸다. 이때 y는 훈련데이터 선택에 따라 영향을 받는 확률변수로 생각할 수 있다. 그리고 최종 예측값은 y의 분포(샘플링된 훈련데이터셋들에 따른 y값)에 따라 결정되므로 정확률 또한 y의 분포에 달려있다고 해석할 수 있다.
Bayes Optimality (베이지안 최적화)
L2-norm 을 기준으로 Query point x에 대한 Loss식을 해석해보자.
Conditional distribution p(t | x) (p(t | x) 조건부 확률분포)를 알고 있을때, 어떻게 y 값을 예측할까?

\(E\left [ t^2|x \right ]\) 식이 변환되는 부분은 분산과 평균의 관계로 아래 이미지를 참고하자.

정리된 식을 살펴보면 첫번째는 \(y=y_{*}\)인 경우 0으로 최소화 할 수있다, 하지만 두번째 분산 식은 inherent unpredictability(내재된 불확실성)으로 noise 혹은 Bayes error(베이지안 에러)로 불린다. 에러값이 작을수록 정답일 확률이 높으므로 y의 확률 분포 중 \(y=y_{*}\)일 때가 정답이 확률이 높다.
\(y_{*}\)값을 선택하는 과정이 Decision theory(의사결정 이론)의 예시 중 하나이다.
Decision theory는 가장 높은 효율을 보이는 방향으로 선택하는 기법을 의미한다.
위의 식은 train data의 특정 확률변수 x에 대해 loss 값을 계산 후 전개한 식이다. 모든 train data로 확장하여 전체 loss값을 구하고 비슷한 과정으로 한번 더 분해해 보자.


최종 Loss 식 분해 결과
- 예측 결과값이 \(y_{*}\)에 얼마나 가까운지를 나타내는 편향
- \(y\) 확률분포의 분산
- 베이지안 에러
다른관점으로 편향(bias)과 분산(variance)은 Underfitting 과 Overfitting에 비교되기도 한다.

- High Bias 는 Underfitting으로 인해 모델이 너무 단순해져 예측 data에 대한 정확한 값을 표현하지 못해 나타난다.
- Low Variance는 Train data의 부족으로 안정적인 결정경계를 만들기 부족한 상황을 의미한다.
- Low Bias는 Train data에 대한 값을 모두 기억하여 예측값 오차가 작아지므로 Overfitting이 되었다고 의심 할 수 있다.
- High Variance라고 항상 좋은건 아니다. Train 에선 좋아보일지라도 Overfitting에 의해 Test에선 낮은 정확률을 보일 수 있다.
Bagging(배깅, Bootstrap Aggregation)
베이지안 최적화에서 편향/분산 분해 값 중 분산을 줄임으로써 총 Loss 값을 줄이는 기법
Train data를 Bootstrap 기법을 이용해 각각 독립인 m개 집합으로 만들 수 있다. (각 train set들이 data가 겹치지 않는다는 뜻)
Bootstrap은 단순복원 임의추출법(random sampling)을 활용하는 기법으로 \(P_{data}\)에서 독립적으로 데이터를 추출 후 중복을 허용하여 원래 데이터의 크기만큼 증강시켜 새로운 데이터 셋을 만드는 방법이다.
각 Train data 들을 기반으로 학습시킨 모델들로 예측한 결과는 평균으로 표현 가능하다.
\(y = \frac{1}{m}\sum_{i=1}^{m} y_{i}\)
이 식이 Loss 식에 어떤 영향을 미치게 될까?
- 베이지안 에러 : 영향받지 않음
- 편향 : \(E\left [ y \right ] = E\left [ \frac{1}{m}\sum_{i=1}^{m}y_{i} \right ] = E\left [ y_{i} \right ]\)
예측값들의 평균은 결국 최종 예측값과 같다. 영향받지 않음 - 분산 : \(Var\left [ y \right ] = Var\left [ \frac{1}{m}\sum_{i=1}^{m}y_{i} \right ] = \frac{1}{m^2}\sum_{i=1}^{m}Var\left [ y_{i} \right ] = \frac{1}{m}Var\left [ y_{i} \right ]\) m으로 나눈만큼 분산값이 줄어듬.
Limit
- 실제 데이터에서 학습데이터 분포에 대해 알 수 있는 방법이 없다.
- 독립인 Train set m개를 나눌만큼 충분한 데이터를 모으기 힘들다.
- 훈련데이터셋들이 모두 독립이 아닐 수 있다. (\(\sigma\)는 표준편차, \(\rho\)는 상관계수 의미)
\(Var\left ( \frac{1}{m}\sum_{m}^{i=1}y_{i} \right ) = \frac{1}{m}(1-\rho )\sigma ^{2}+\rho\sigma^{2}\)
Solution : bootstrap aggregation, or bagging
- Take a single dataset \(D\) with n examples
- Generate m new datasets, each by sampling n training examples from \(D\)
- Average the predictions of models trained with m Train datasets
- 모든 데이터셋들이 서로 독립이 되기는 어려우므로 다른 종류의 모델을 사용함으로써 모델 예측값의 독립성을 높임 (\(\rho\)줄임)
Random Forest
- 다른 종류의 모델을 사용하는 대표적인 방식
- 독립적으로 훈련된 이진 결정트리의 집합(Collection of independently-trained binary decision trees)
- 가장 좋은 블랙박스 머신러닝 알고리즘 중 하나(Random forests are probably the best black-box machine learning algorithm)
Example



Summary
- 배깅은 예측값들을 평균으로 나누며 과적합 방지
- 한계 : Loss식에서 보았듯이 분산은 줄이지만 편향은 줄이지 못함
- 여전히 분류기와 상관관계가 존재
- Random Forest 해결법 : 더 많은 랜덤성을 부여
Boosting
분류기(모델)들을 순차적으로 연결하고 이전에 잘 예측하지 못한 값을 중점으로 학습하여 Bias값 축소를 통해 Loss를 줄이는 기법
What is Weak Learner/Classifier?
A learning algorithm that outputs a hypothesis (e.g., a classifier) that performs slightly better than chance. (이진분류 추측보다 조금 더 나은 모델)
Example : Decision Trees, Decision Stump
Weak Classifier \(h(w = (w_{1}, ~ ,w_{N} with \sum_{N}^{i=1}w_{i}=1, w_{i}\geq 0)\)에 대한 error식은 아래와 같다.
\(err = \sum_{N}^{i=1}w_{i}\mathbb{I}\left\{h(x_{i})\neq y_{i} \right\}\) is at most \(\frac{1} {2} - \gamma, \gamma>0\)
Weak Classifier는 모델이 너무 단순하여 손실값을 효율적으로 줄이지 못한다. Boosting은 이 문제점을 어떻게 해소할까?
AdaBoost(Adaptive Boosting)
적응형 boosting으로 약한 분류기를 순차적으로 연결하고 순서마다 오답률이 높은 데이터를 중심으로 학습하여 성능을 높여가는 기법.
각 분류기 결과를 선형결합하여 최종 예측값을 내놓는다.
steps
- At each iteration we re-weight the training samples by assigning larger weights to samples (i.e., data points) that were classified incorrectly. (매 반복마다 오답인 데이터들의 가중치를 높게 설정한다.)
- We train a new weak classifier based on the re-weighted samples. (설정된 가중치를 기준으로 새로 뽑은 데이터들로 다시 학습한다.)
- We add this weak classifier to the ensemble of classifiers.This is our new classifier. (약한 분류기들을 연결한 전체가 하나의 강한 분류기가 된다.)
- Weight each weak classifier in the ensemble with some weights.
- We repeat the process many times. (위 과정을 반복한다.)
AdaBoost reduces bias by making each classifier focus on previous mistakes. 이전 실수를 집중적으로 줄임으로써 편향값을 줄이고 이는 Loss값이 줄어 전체적인 성능이 올라가게 된다.
Example
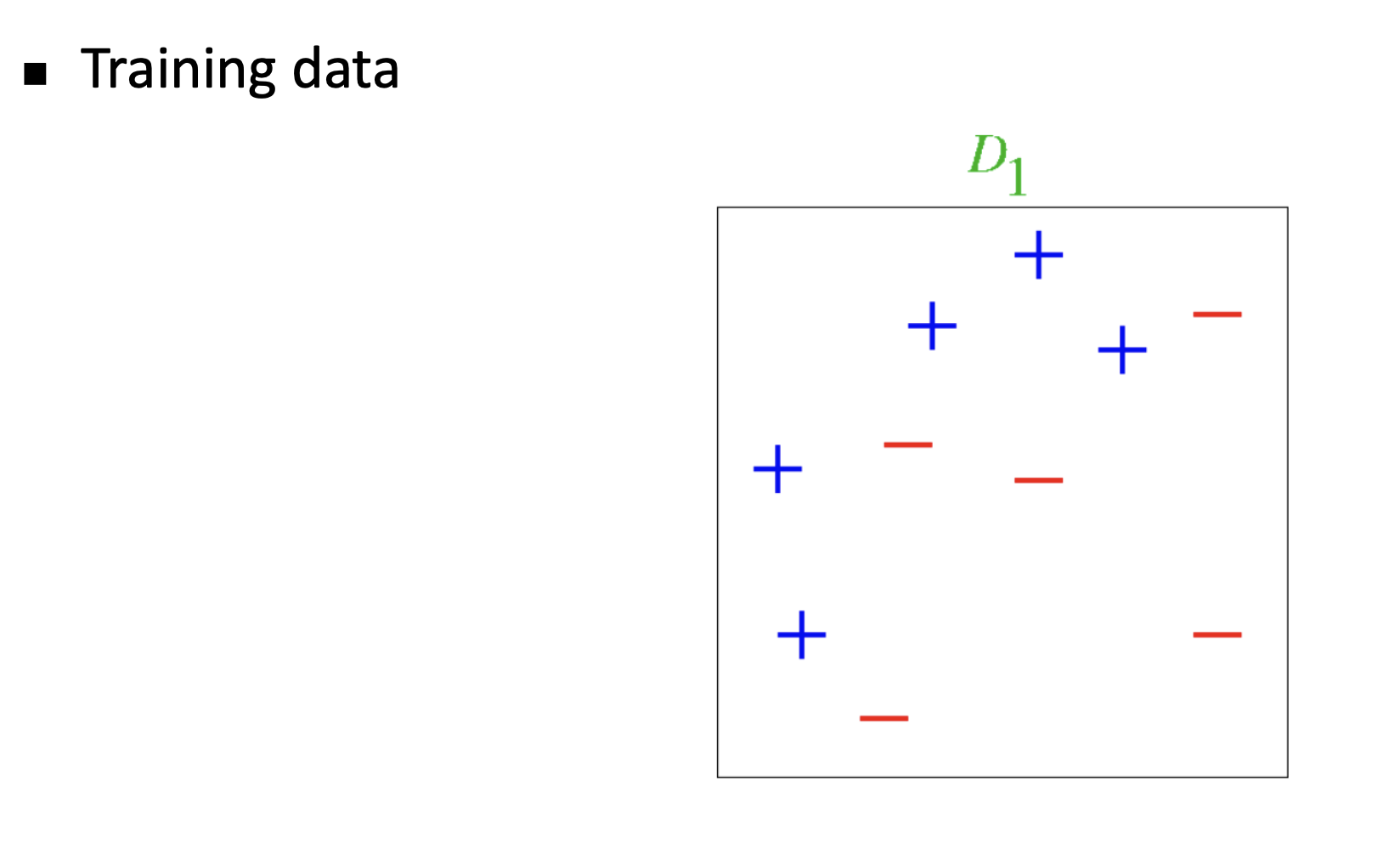
해당 데이터를 AdaBoost를 이용해 분류하고자 한다고 해보자.
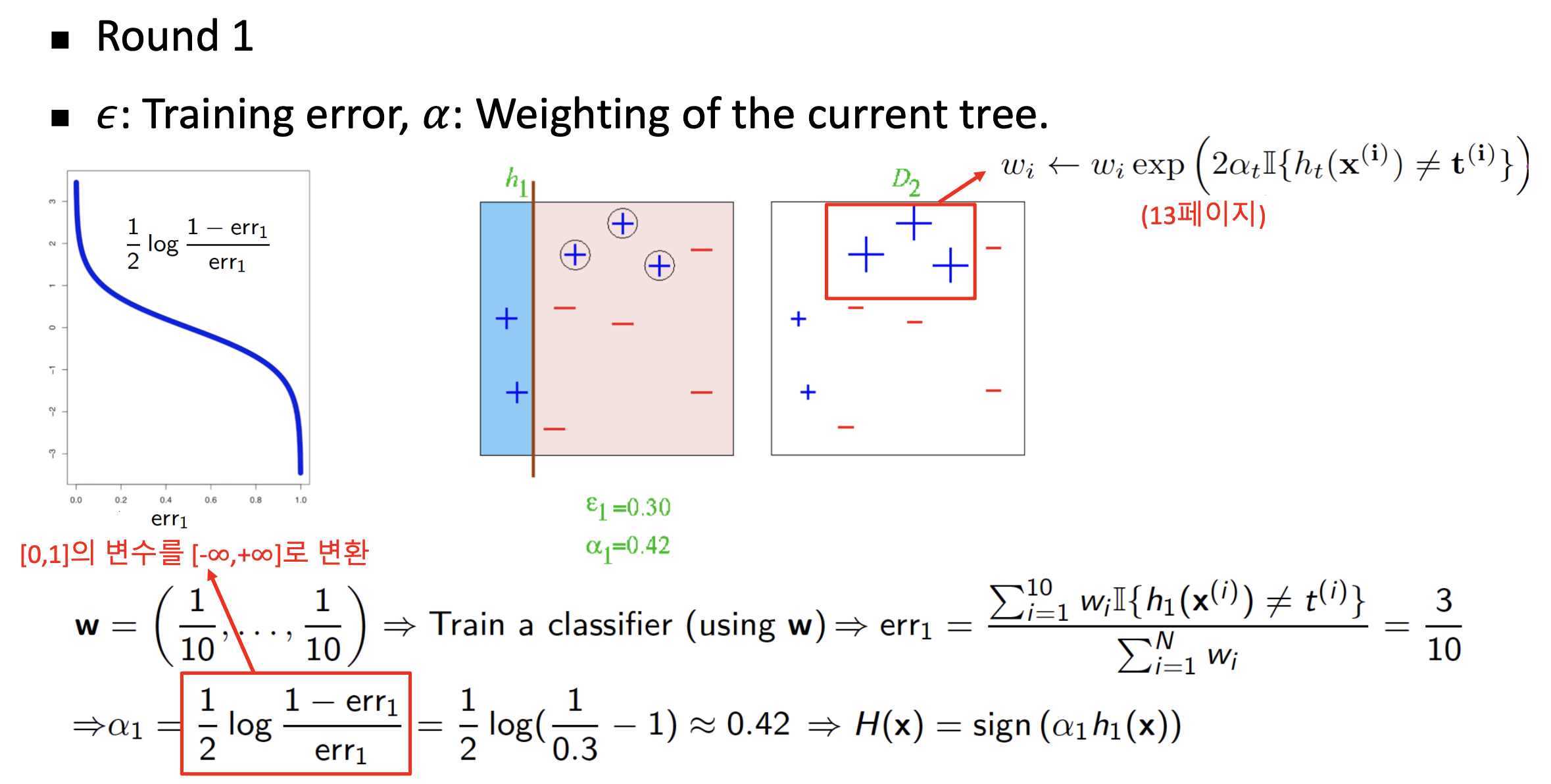
- \(h_{1}(x)\)이 첫번째 약한 분류기라고 할때, 그에 대한 Error(Loss)값 계산
- Error식에는 \(\mathbb{I}\)가 있는데 이는 항등 함수로 분류기가 맞추지 못한 경우 1 나머지는 0을 반환
- \(\alpha_{1}\)을 계산하고 샘플 가중치 갱신

- 갱신된 가중치를 기준으로 데이터를 복원 추출하고 맨처음 가중치로 원상복구
- Round1 과정 M번까지 반복 (그 이전에 일정 수치 이상의 정확률이 나올시 조기 종료 가능)


- 반복하는 횟수 M이 3이라고 하였을때 위와 같은 최종 분류기 형태가 완성
- 예측방법은 각 분류기 결과에 가중치\(\alpha_{i}\)를 곱해 합한 결과를 sign함수에 넣어 1이면 참 -1이면 거짓 판별
AdaBoost Algorithm


위 식은 AdaBoost가 training error값을 줄이고 단순 이진분류보다 낫다는 점을 설명한다.
AdaBoost의 Error분석

- 학습을 오래하면 과적합을 일으킬 확률이 높다
- 약한 분류기를 계속 추가할경우 전체 분류기는 복잡해져 과적합이 발생할 수 있다
- AdaBoost 는 과적합에 대체로 유연하게 대처하는 특징을 가지고 있다

하지만 그렇지 않은 경우도 존재한다. 위 경우는 어떻게 일어나는걸까?
주어진 train set에 대해 분류가 완벽히 되어 train error는 0이 되었더라도 결정경계나 데이터간의 거리에 대해 더 최적화되는 과정일 수 있다.
AdaBoost Example
- Face Detection



Summary
- Boosting은 약한 분류기간의 조합을 통해 bias를 줄여 성능 높임
- 각 분류기는 이전 분류기를 기준으로 새로 학습
- 과적합에 강하게 대응하지만 AdaBoost도 충분히 과적합 가능
- 주어진 Dataset 분포에 많이 의존하는 경향
- 약한 분류기는 Decision Stump 외에도 상관없이 대체 가능
Additive Models
A hopothesis class \(H\) with each \(h_i :x \mapsto \{ -1,+1 \} \; within \; H, i.e.,h_i \in H\)
It's called "weak learners", "bases"
\( H_m(x)=\sum_{(i)}^m\alpha_ih_i(x), where (\alpha_1,\cdots,\alpha_m)\in R^m \)
Boosting : linear combination of base classifiers
Greedy approach to train Additive Models
- Initialize \(H_0(x)=0\)
- For m = 1 to T:
Compute the m-th hypothesis and its coefficient
\((h_m,\alpha_m) \leftarrow \underset{h \in H,\alpha}{argmin}\sum^N_{i=1}L(H_{m-1}(x^{(i)})+\alpha h(x^{(i)}),t^{(i)})\)
이전 분류기에 가중치가 곱해진 예측과 현재 분류기의 예측값 합이 최종 예측값이 되고 그에 해당하는 Loss가 가장 작은 \(H,\alpha\)를 구한다. - Add it to the additive model
\(H_m=H_{m-1}+\alpha_mh_m\)
다음 분류기에 가중치를 곱해 분류기를 수정, 최신화한다.
Consider the exponential loss (Adaboost)
\(L_E(y,t)=exp(-ty)\)
\((h_m,\alpha_m) \leftarrow \underset{h \in H,\alpha}{argmin}\sum^N_{i=1} exp(-[(H_{m-1}(x^{(i)})+\alpha h(x^{(i)})]t^{(i)})\)
\(=\sum^N_{i=1} exp(-H_{m-1}(x^{(i)})t^{(i)}-\alpha h(x^{(i)})t^{(i)})\)
\(=\sum^N_{i=1} exp(-H_{m-1}(x^{(i)})t^{(i)})exp(-\alpha h(x^{(i)})t^{(i)})\)
Here we define \(w^{(m)}_i \overset{\Delta}{=}exp(-\alpha h(x^{(i)})t^{(i)})\)
\(=\sum^N_{i=1} w^{(m)}_i exp(-\alpha h(x^{(i)})t^{(i)})\)
\((h_m,\alpha_m) \leftarrow \underset{h \in H,\alpha}{argmin}\sum^N_{i=1} w^{(m)}_i exp(-\alpha h(x^{(i)})t^{(i)})\)
If \(H(x^{(i)})=t^{(i)}, exp(-\alpha h(x^{(i)})t^{(i)})=exp(-\alpha)\)
If \(H(x^{(i)}) \neq t^{(i)}, exp(-\alpha h(x^{(i)})t^{(i)})=exp(+\alpha)\)
맞은 경우는 부호가 서로 같고 틀린 경우는 부호가 다르게 나오기 때문에 위와같은 결과가 나온다.
\(\sum^N_{i=1} w^{(m)}_i exp(-\alpha h(x^{(i)})t^{(i)})\)
\(=e^{-\alpha} \sum^N_{i=1} w_i^{(m)} \mathbb{I} \{ h(x^{(i)})=t_i \} + e^{\alpha} \sum^N_{i=1} w_i^{(m)} \mathbb{I} \{ h(x^{(i)}) \neq t_i \} \)
\(=(e^{\alpha}-e^{-\alpha}) \sum^N_{i=1} w_i^{(m)} \mathbb{I} \{ h(x^{(i)})\neq t_i\} + e^{-\alpha} \sum^N_{i=1} w_i^{(m)}[\mathbb{I} \{ h(x^{(i)}) \neq t_i \} + \mathbb{I} \{ h(x^{(i)}) = t_i \} ] \)
\( Since \; [\mathbb{I} \{ h(x^{(i)}) \neq t_i \} + \mathbb{I} \{ h(x^{(i)}) = t_i \}] = \mathbb{I} \)
\(=(e^{\alpha}-e^{-\alpha}) \sum^N_{i=1} w_i^{(m)} \mathbb{I} \{ h(x^{(i)})\neq t_i\} + e^{-\alpha} \sum^N_{i=1} w_i^{(m)}\)
Optimize h:
We have to minimize above loss equation
The first term on the RHS \((e^{\alpha}-e^{-\alpha}) \geq 0\) => omit
The second term on the RHS does not depend on h => delete
\(h_m \leftarrow \underset{h \in H}{argmin} \sum^N_{i=1} w_i^{(m)}exp(-\alpha h(x^{(i)})t^{(i)}) \equiv \underset{h \in H}{argmin} \sum^N_{i=1} w_i^{(m)} \mathbb{I}\{ h(x^{(i)}) \neq t_i \} \)
Loss값이 커지는 요소는 예측이 틀렸을 경우가 크게 차지하므로 이 부분을 중점적으로 줄이면 된다.
Find \(\alpha\):
Define weighted classification error: \(err_m = \frac{\sum^N_{i=1} w_i^{(m)} \mathbb{I}\{ h(x^{(i)}) \neq t_i \}}{\sum^N_{i=1} w_i^{(m)}}\)
전체 예측 예측값을 분모로하고 분자는 예측이 틀린경우의 확률값을 더한다.
Opimize \(h_m\)에 대한 식을 \(\alpha\)를 고려하여 작성 할 수있다.
\( \underset{h \in H}{min} \sum^N_{i=1} w_i^{(m)}exp(-\alpha h(x^{(i)})t^{(i)})=\underset{h \in H}{argmin} \sum^N_{i=1} w_i^{(m)} \mathbb{I}\{ h(x^{(i)}) \neq t_i \} \)
Then we have,
\(\underset{\alpha}{min} \underset{h \in H}{min} \sum^N_{i=1} w_i^{(m)}exp(-\alpha h(x^{(i)})t^{(i)})\)
\(=\underset{\alpha}{min} \; \{ (e^{\alpha}-e^{-\alpha})\sum^N_{i=1} w_i^{(m)} \mathbb{I}\{ h(x^{(i)}) \neq t_i \} +e^{-\alpha} \sum^N_{i=1} w_i^{(m)} \} \)
By definition of the \(err_m\)
\(=\underset{\alpha}{min} \; \{ (e^{\alpha}-e^{-\alpha})err_m(\sum^N_{i=1} w_i^{(m)})+e^{-\alpha}(\sum^N_{i=1} w_i^{(m)}) \} \)
Derivative above the objcetive function w.r.t. \(\alpha\) and set zero to find global minimum
\(\frac{\partial L}{\partial \alpha}=(e^{\alpha}+e^{-\alpha})err_m(\sum^N_{i=1}w_i^{(m)})-e^{-\alpha}(\sum^N_{i=1}w_i^{(m)})=0\)
\((e^{\alpha}+e^{-\alpha})err_m-e^{-\alpha}=0\)
\((e^{2\alpha}+1)err_m-1=0\)
\(e^{2\alpha}err_m=1-err_m\)
\(e^{2\alpha}=\frac{1-err_m}{err_m}\)
\(\alpha = \frac{1}{2}log(\frac{1-err_m}{err_m})\)
Update weight
\(w_i^{(m+1)}=exp(-H_m(x^{(i)})t^{(i)})\)
\(=exp(-[H_{m-1}(x^{(i)})+\alpha_m h_m(x^{(i)})]t^{(i)})\)
\(=exp(-H_{m-1}(x^{(i)})t^{(i)})exp(\alpha_m h_m(x^{(i)})t^{(i)})\)
\(=w_i^{(m)}exp(\alpha_m h_m(x^{(i)})t^{(i)})\)
\(=w_i^{(m)}exp(\alpha_m(2\mathbb{I} \{ h_m(x^{(i)})=t^{(i)} \} -1 ))\)
\(=exp(\alpha_m)w_i^{(i)}exp(-2\alpha_m \mathbb{I} \{ h_m(x^{(i)})=t^{(i)} \})\)
\(exp(\alpha_m)\) term은 모든 sample에 곱하는 가중치로 loss minimization에는 영향이 없다.
Summary
\(H_(x)=\sum^m_{i=1}\alpha_i h_i(x)\)
\(h_m \leftarrow \underset{h \in H}{argmin}\sum_{i=1}^N w_i^{(m)} \mathbb{I}\{ h(x^{(i)}) \neq t_i \} \)
\(\alpha = \frac{1}{2}log(\frac{1-err_m}{err_m}), where \; err_m=\frac{\sum^N_{i=1} w_i^{(m)} \mathbb{I}\{ h(x^{(i)}) \neq t_i \}}{\sum^N_{i=1} w_i^{(m)}}\)
\(w_i^{(m+1)}=w_i^{(m)}exp(-\alpha_m h_m (x^{(i)})t^{(i)})\)
When we set loss function to exponential loss, derived AdaBoost algorithm.
'Machine Learning' 카테고리의 다른 글
| What is Linear Classification? [Ⅰ] (0) | 2022.12.17 |
|---|---|
| What is Linear Regression? (0) | 2022.10.12 |
| What is Decision Trees? (3) | 2022.09.19 |
| What is Nearest Neighbor? (0) | 2022.09.10 |




