ROKO
What is Linear Classification? [Ⅰ] 본문
Classification : Predicting a discrete-valued target
- Binary class (pos / neg, 0/1, true/false)
- Multiclass
Binary linear classification
linear model
\(z = w^{T}x + b \)
\(y=\left\{\begin{matrix} 1 \; if \; z \geq r\\ 0 \; if \; z < r \end{matrix}\right.\)
w 가중치와 x를 곱하고 편향을 더한 결과가 임계값을 넘냐 아니냐로 분류를 할 수 있다.
조금 더 식을 정리 할 수 없을까?
\(w^{T}x+b\geq r \Leftrightarrow w^{T}x+b-r\geq 0\)
상수부분을 하나로 묶어서 치환하자 그러면 위와 같이 정리가 된다. 추가로 편항의 덧셈까지 행렬의 곱셈으로 포함시키면 더 식이 간략화 된다.
\((Weight)\times(Data) + (bias) = (Weight, bias)\times(Data, 1)\)
- Add dummy feature \(x_{0}\) which take value 1
- Add bias \(w_{0}\) to w
\(z = w'^{T}x' \)
\( y =\left\{\begin{matrix} 1 \; if \; z \geq 0 \\ 0 \; if \; z < 0 \end{matrix}\right.\)
Geometric view

\( w_{0}x_{0} > 0 \Leftrightarrow w_{0} > 0\)
\(w_{0}x_{0} + w_{1}x_{1} < 0 \Leftrightarrow w_{0} + w_{1} < 0 \)
위를 바탕으로 적당한 \(w_{0}, w_{1}\)를 설정해보자.

Hypotheses w 는 half-spaces로 설명됨을 알 수 있다.
\( H_{+} = {x : w^{T}x \geq 0} \)
\( H_{-} = {x : w^{T}x < 0} \)
여기서 +,-의 부호 결정에 의문점이 생길 수 있다. input space의 data와 weight의 w의 계산을 내적의 관점에서 바라보면 t=1 인 경우는 내적의 값이 0 이상이고 t=0 인 경우는 그 반대가 된다.
이 결과를 보고 부호를 결정하는데 두 데이터를 분류함에 목적이 클뿐 어느쪽이 +,- 인지는 따지지 않아도 된다.
두 분류 공간이 겹치는 부분을 decision boundary(결정경계)라고 부른다. \( \left\{x : w^{T}x = 0 \right\} \)
예시는 이진분류를 2차원 공간에서 나타내었기에 직선인 boundary가 생성되지만 일반화한 hyperplane(초평면)에서는 다른 차원의 결정경계가 생길 수 있다. 결과적으로는 linear decision boundary가 생성된다.
input space의 경우를 모두 만족하는 weight space는 feasible region 이라고 불린다. 이때 weight space = nonempty (존재)이면 feasible하다고 부른다.
Limits of Linear classification
그렇다면 Linear Regression 은 모든 input space에 대해서 linear seperable할까?
NO!
Ctex (1)

선형 분류가 불가능함을 직관적으로 알 수 있다.
How to ovecome this XOR limit?
Expand feature dimension
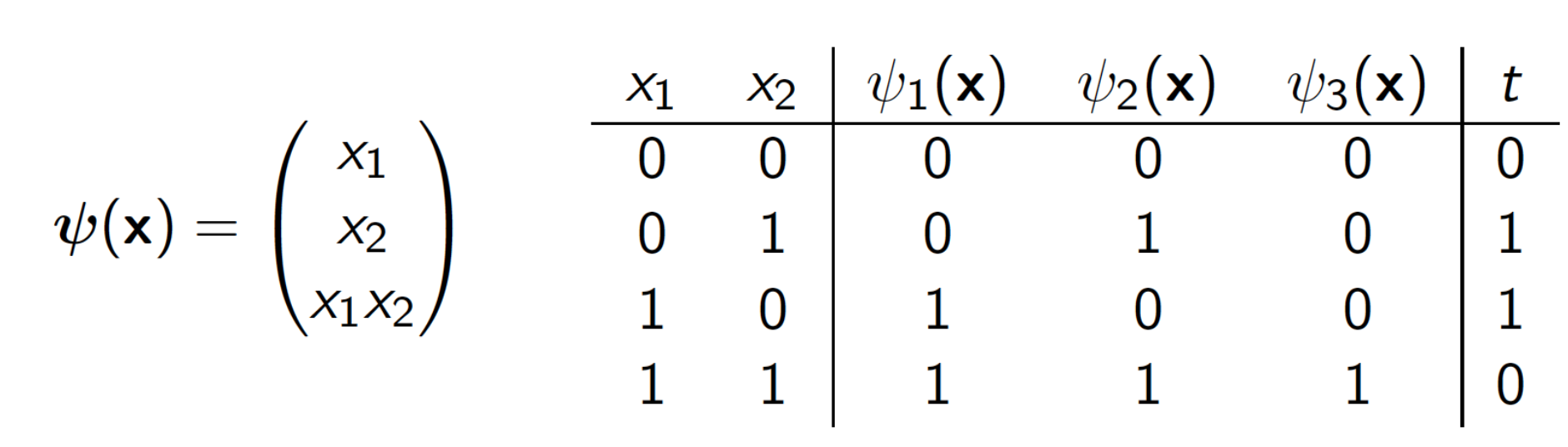
2차원에서 선형분류가 불가하므로 차원을 추가해 3차원에서 선형 분류를 시도한다. 위의 data룰 기준으로 찾으면 선형 분할이 가능한 평면방정식을 찾을 수 있다. 오해하면 안되는 부분은 선형 분류에서 선형이란 직선을 의미하는 것이 아닌 linear transformation[link]을 만족하는 것을 의미한다. 선형성을 띄는 함수들은 예측이 가능하다고 이해하면 편하다.
위와같이 feature map의 차원을 확장해 선형 분류를 할 수도 있고, 오히려 차원을 줄이는 방법도 있다. (MLP, PCA, SVD, etc)
Ctex (2)

4x4 image를 1-dimension vector 표현 한것이다. 우리는 사진의 물체가 옆으로 이동한다고 하더라도 사물을 인식하는데 큰 어려움이 없다. 하지만 컴퓨터는 이미지를 위와 같은 배열로 이해하는데, image A, B에 대해 값이 1로 통일된 weight에 대해 각 pattern A,B의 특징 평균을 매기면 A에는 16칸중 4개의 칸이 검은색 B 또한 16개의 칸중 4개의 칸이 검은색으로 같은 특징값으로 추출된다.
하지만 pattern A, B는 엄염히 다른 images로 인식되어야 한다. 이는 computer vision 분야에서 다루는 문제 중 하나이다.
How to find proper weight, bias?
- Define loss function to minimize cost function
0-1 Loss
\( L_{0-1}(y,t) = \left\{\begin{matrix} 0 \; if \; y=t \\ 1 \; if \; y \neq t \end{matrix}\right. =\mathbb{I}[y \neq t] \)
error rate : \(J = \frac{1}{N}\sum_{i=1}^{N}\mathbb{I}[y^{(i)} \neq t^{(i)}]\)
visualization of cost function in weight space

How to optimize?
Generally, it's hard problem
(Guruswami and Raghavendra)
“For arbitrary 𝜖, 𝜎 > 0, we prove that given a set of examples-label pairs from the hypercube a fraction 1 − 𝜖 of which can be explained by a halfspace, it is NP-hard to find a halfspace that correctly labels a fraction"(1/2 + 𝛿 of the examples."
hypercube의 1-𝜖 비율 만큼의 정제된 데이터(data - label)가 있을때 (1/2+ 𝛿 )만큼 데이터를 정확히 분류 할 수 있는 halfspace를 찾는 것은 NP-hard(Algorithm 용어로 다항식의 시간 내에 풀 수 없음을 의미) 문제이다.
Solution : Gradient descent with chain rule
\( \frac{\partial L_{0-1}}{\partial w_{j}}=\frac{\partial L_{0-1}}{\partial z}\frac{\partial z}{\partial w_{j}}\)

Problem!
- 0-1 Loss function의 미분값은 항상 0이다.
- gradient descent가 학습되지 않는다.
- z = 0 일때 gradient가 존재하지 않는다.(infinity, overflow)
- 불연속 함수 (uncontinious function)
Solution : Surrogate loss function (0-1 Loss에 근사하는 continous function 설계)
Squared error loss
\(L_{SE}=\frac{1}{2}(y-t)^2\)
\(L_{SE}\) can be derivative, and also \(\frac{\partial L_{SE}}{\partial w} \neq 0, \frac{\partial L_{SE}}{\partial w}=y-t\)
y값의 label을 판단하는 threshhold로 \(y = \frac{1}{2}\)이 사용된다, 쉽게말해서 t 가 0이냐 1이냐를 \(y = \frac{1}{2}\)를 기준으로 이상이면 t=1, 이하면 t=0으로 여긴다는 뜻이다.
But, there is another problem!

residual problem \(y = \frac{1}{2}\)인 y값들 중에서 높은 확신으로 y=100이 나왔다고 가정하고 t=1이 참이라고 가정하자. 정답임에도 불구하고 loss function의 값에 높은 오차로 여겨져 error rate에 포함된다. 우리는 틀린 경우에 해당하는 결과에 대해서만 error값을 수집하기를 원하므로 이를 해결해여 한다.
Solution : Use Logsitic Activation Function (sigmoidal or S-shaped function)
Sigmoid
\(\delta (z) = \frac{1}{1+e^{-z}}\)
Log-linear (a linear model with a logistic nonlinearity)
\(z = w^{T}+b \)
\(y = \delta (z) \)
\(L_{SE} = \frac{1}{2}(y-t)^{2}\)
Here, we say "\(\delta\)" is an activation function, and "\(z\)" is called the logit.
Another problem, not learning at some y value during gradient descent stage
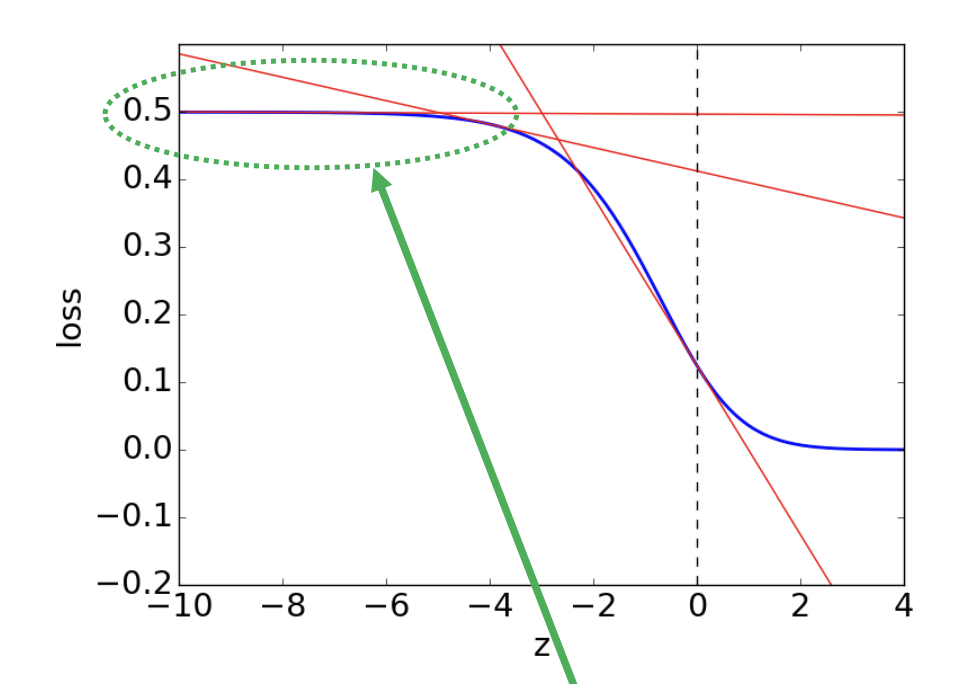
우리는 back propagation에서 \(w_{j} = w-{j} - \alpha \frac{\partial L}{\partial w_{j}}\) 로 update되는데 위 그림의 초록색 화살표를 따라가며 관찰했을때, threshhold로부터 조금만 떨어져도 \(\frac{\partial L}{\partial \delta} \frac{\partial \delta}{\partial w_{j}} \approx 0\) 이 되어 weight parameter update가 거의 진행되지 않는다.
다시말해서 잘못한 예측이 많아 error값이 클 경우 초록색 구간에 해당할 것이고 미분값이 0에 근사하여 가중치(weight)가 갱신되지 않는다. Also, we want to impose more penalty about more wrong expectation.
Solution : Cross entropy Loss
\(L_{CE}(y,t) = \left\{\begin{matrix} -log y \; if \; t=1 \\ -log(1-y)\; if \; t=0 \end{matrix}\right.= -tlogy-(1-t)log(1-y)\)

\( z = w^{T}x+b \)
\( y = \delta (z) = \frac{1}{1+e^{-z}} \)
\(L_{CE} = -tlog(y)-(1-t)log(1-y)\)
\(\frac{\partial L}{\partial w_{j}} = \frac{\partial L}{\partial \delta} \frac{\partial \delta}{\partial w_{j}} = y-t\)
WHY? check this proof[link]
Last problem
If t=1 but model predict very wrong than y is close to numerically zero,then need to compute log 0.
It causes hard-to-bugs. We have to make y does not close to zero or one. (Look above CE graph)
Solution : logistic-cross-entropy (combine the activation function and the loss function)
Logistic-Cross-Entropy
\(L_{LCE}(z,t) = L_{CE}(\delta (z),t)=tlog(1+e^{-z})+(1-t)log(1+e^{z})\)
\(\frac{\partial L}{\partial w_{j}} = \frac{\partial L}{\partial \delta} \frac{\partial \delta}{\partial w_{j}} = y-t\)
WHY? check this proof[link] (Similar as \(L_{CE}\))
It looks same as \(L_{CE}\), but when we compute t=1, z=-infinity \(L_{LCE}\) does not cause log 0 because of combination of loss and activation.
In detail log 0 is caused by \(\delta (z)\), large denomiator(분모) . Look at the above equation \(L_{LCE}\), \(-tlog\frac{1}{1+e^{-z}}-(1-t)log(1-\frac{1}{1+e^{-z}})\) become reciprocal(역수) to \(tlog(1+e^{-z})-(1-t)log(1+e^{z})\).
#Python code with numpy
import numpy as np
E = t * np.logaddexp(0,-z) + (1-t) * np.logaddexp(0,z)Comparison of loss functions:

Comparison of gradient descent upadates :
- Linear regression
\(w \leftarrow w-\frac{\alpha}{N}\sum_{i=1}^{N}(y^{(i)}-t^{(i)})x^{(i)}\) - Logistic regression
\(w \leftarrow w-\frac{\alpha}{N}\sum_{i=1}^{N}(y^{(i)}-t^{(i)})x^{(i)}\)
Equations look same, but it's not a coincidence meaning!
These functions are called matching loss functions. [Talk about later]
'Machine Learning' 카테고리의 다른 글
| What is SVMs? (2) | 2022.12.20 |
|---|---|
| What is Linear Classification? [Ⅱ] (0) | 2022.12.19 |
| What is Linear Regression? (0) | 2022.10.12 |
| Ensemble (Bagging, Boosting) (0) | 2022.10.10 |




