ROKO
What is Linear Classification? [Ⅱ] 본문
Gradient Checking
우리는 backpropagation 과정에서 weight update를 위해 direct derivative를 계산해야한다. 하지만 미분 불능의 경우도 존재하기에 근사식을 사용해 적용하게 되는데 미분값 오차가 있는지 없는지 검증하는 과정이 필요하다.
Finite differences (유한차분)
Let \(h\) be small value, e.g. \(10^{-10}\)
\(\frac{\partial}{\partial x_{i}}f(x_{1},\cdots,x_{N})=\displaystyle \lim_{h \to 0}\frac{f(x_{1},\cdots,x_{i}+h,\cdots,x_{N})-f(x_{1},\cdots,x_{i},\cdots,x_{N})}{h}\)
Generally, the two-sided definition is better, accurate
\(\frac{\partial}{\partial x_{i}}f(x_{1},\cdots,x_{N})=\displaystyle \lim_{h \to 0}\frac{f(x_{1},\cdots,x_{i}+h,\cdots,x_{N})-f(x_{1},\cdots,x_{i}-h,\cdots,x_{N})}{2h}\)
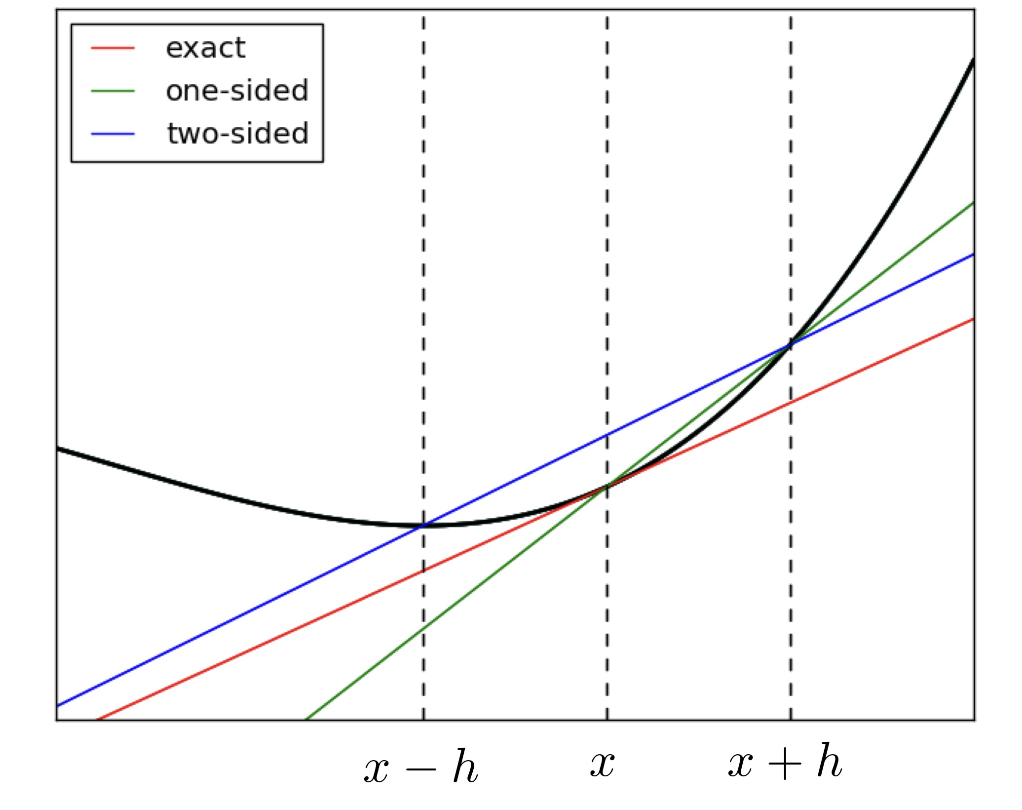
또한 위 그래프를 관찰하면 실제 미분 기울기(red)와 가장 근사한 방식은 forward finite difference method(Green)나 backward finite difference method도 아닌 central finite difference(blue)임을 알 수 있다.
Relative Error
(derived gradient and finite difference approximation)
\(\frac{|a-b|}{|a|+|b|}\)
The relative error should be small, e.g. \(10^{-6}\)
Learning rate (\(\alpha\))
\(w = w-\alpha \frac{\partial L}{\partial w}\)
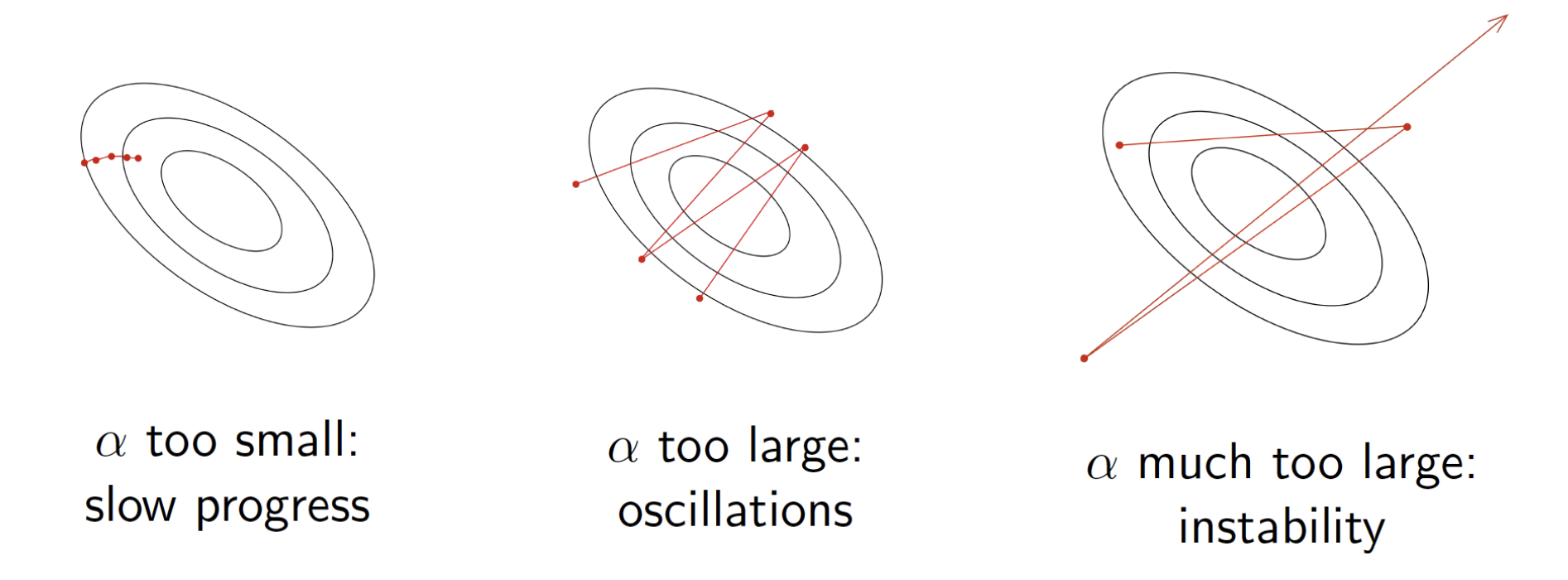
Purpose : find proper \(\alpha\) to model for good performance
How to find?
- Grid search
- Use large learning rate and gradually decay the learing rate to reduce the fluctuations.
How to know?
- Training curves
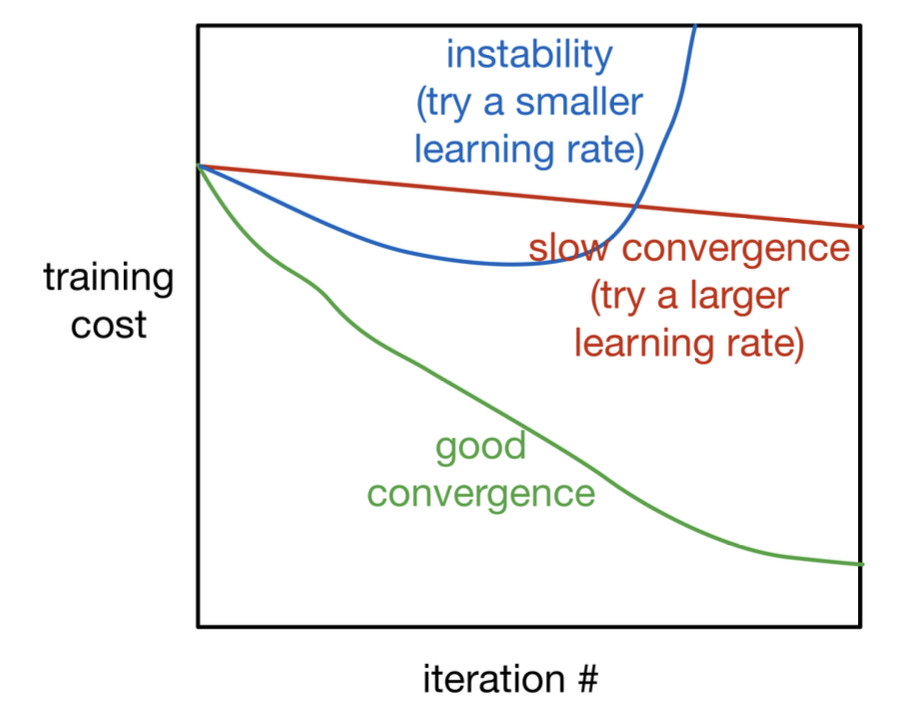
Be careful! Training curves and validation curves are different each other!
Trade-off
Learning rate is too small
- slow to converge
- need much time
- Local minimum problem
Learning rate is large
- lflucutuates
- fast to converge
- can't fit detail
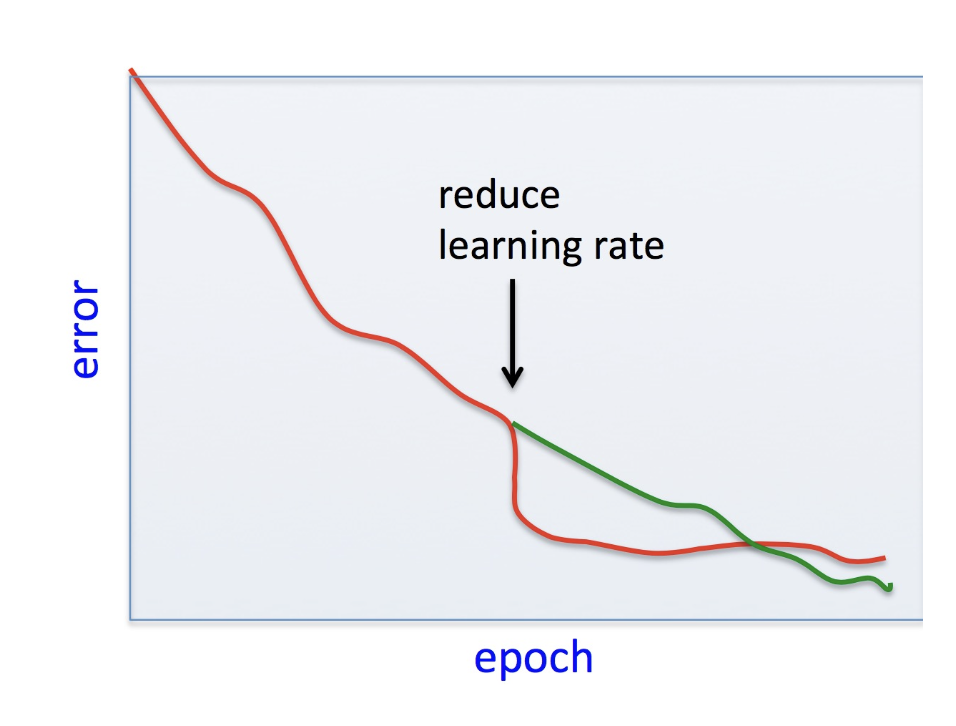
Solution : Early stopping
- Drop learing rate during training time when the convergence is too slow or accuracy does not increase.
[Talk about later]
Gradient descent
1. Stochastic Gradient Descent (SGD)
Average Loss function \(J(\theta)=\frac{1}{N}\sum_{i=1}^{N}L(y(x^{(i)},\theta),t^{(i)})\)
\(\frac{\partial J}{\partial \theta}=\frac{1}{N}\sum_{i=1}^{N}\frac{\partial l^{(i)}}{\partial \theta}\)
- Update weight based on gradient for a random single training data
\(\theta \leftarrow - \alpha \frac{\partial L^{(i)}}{\partial \theta}\)
SGD can make siginificant progress even look all dataset. 하지만 하나의 데이터만 본다면 그 데이터들에 대해서만 가중치가 조정되어 과적합이 일어나거나 학습이 잘되지 않을까? 라는 의문이 생길 수 있다.
proof)
\(E[\frac{\partial L^{(i)}}{\partial \theta}]=\frac{1}{N}\sum_{i=1}^{N}\frac{\partial L^{(i)}}{\partial \theta}=\frac{\partial J}{\partial \theta}\)
랜덤 데이터 하나씩 미분계수 값을 계산하여 평균을 내면 전체 데이터의 미분계수와 같음을 알 수 있다.
Problems!
- 데이터를 하나씩 보기 때문에 분산이 크다.
- 벡터연산이 아니라 하나씩 계산하므로 CPU를 사용하는것과 다를바 없다. (Too slow, GPU를 활용한 벡터연산 필요)
2. Batch training
- Update weight based on gradient for a whole training data
\(\theta \leftarrow - \alpha \frac{\partial J}{\partial \theta}\)
모든 데이터에 대해 조정하므로 정확한 방향으로 조정되어 학습율이 증가한다.
Problems!
- 전체 데이터를 한번에 계산하므로 좋은 GPU가 아닌 이상 계산시간이 오래 걸린다.
- 대용량 학습을 진행할 경우 Memory가 부족할 수 있다.
3. Mini-batch training
- Update weight based on gradient for a medium sized set of training data
\(Var[\frac{1}{|M|}\sum_{i \in M}\frac{\partial L^{(i)}}{\partial \theta_{j}}]=\frac{1}{|M|^{2}}\sum_{i \in M}Var[\frac{\partial L^{(i)}}{\partial \theta_{j}}]=\frac{1}{|M|}Var[\frac{\partial L^{(i)}}{\partial \theta_{j}}]\)
The mini-batch size \(|M|\) is a hyperparameter
- Too large : Out of memory, Too slow (Batch problem)
- Too small : Can't vectorization, CPU operation \(\rightarrow\) too slow(Stochastic problem)
- Choose appropriate number M(multiple of 2, e.g. 2,4,8,16,32...)
Why multiple of 2?
- Beacuse of hardware relation, computer has binary operation [Talk about later]
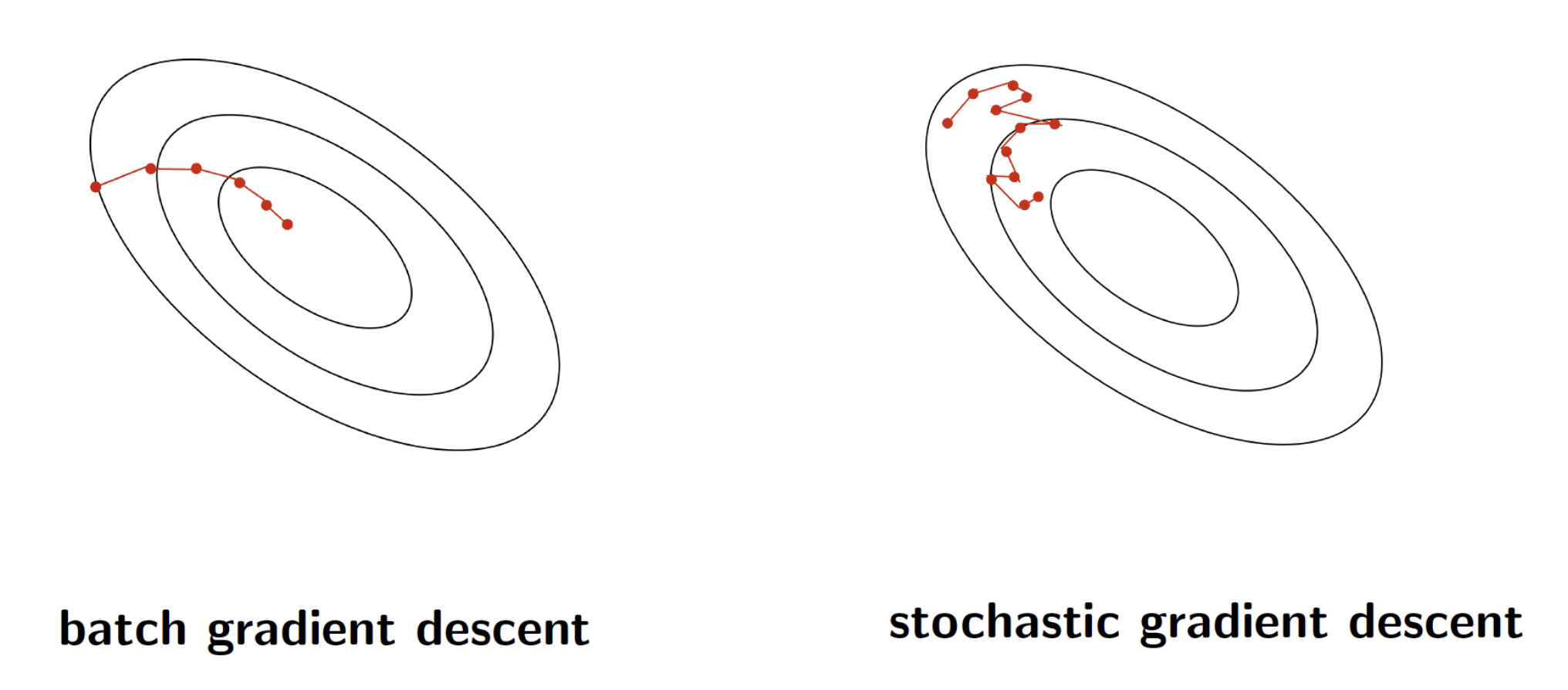
Batch is accurate and slow, Stochastic fluctuates and fast(each data) but whole training time is slow as same as Batch training.
Convexity
A set S is convex if any line segment connecting points in S lies entirely within S.
\(x_{1},x_{2} \Rightarrow \lambda x_{1}+(1-\lambda)x_{2} \in S \; for \; 0 \geq \lambda \leq 1\)
By Mathematical Induction
- weighted averages, convex combinations
\(\lambda_{1}x_{1}+\cdots+\lambda_{N}x_{N} \in S \; for \; \lambda_{i} > 0, \; \lambda_{1}+\cdots+\lambda_{N}=1\)
A function \(\mathbf{f}\) is convex if ant \(x_{0},x_{1}\) in domaibn of \(f\).
\(f((1-\lambda)x_{0}+\lambda x_{1}) \leq (1-\lambda)f(x_{0})-\lambda f(x_{1})\)
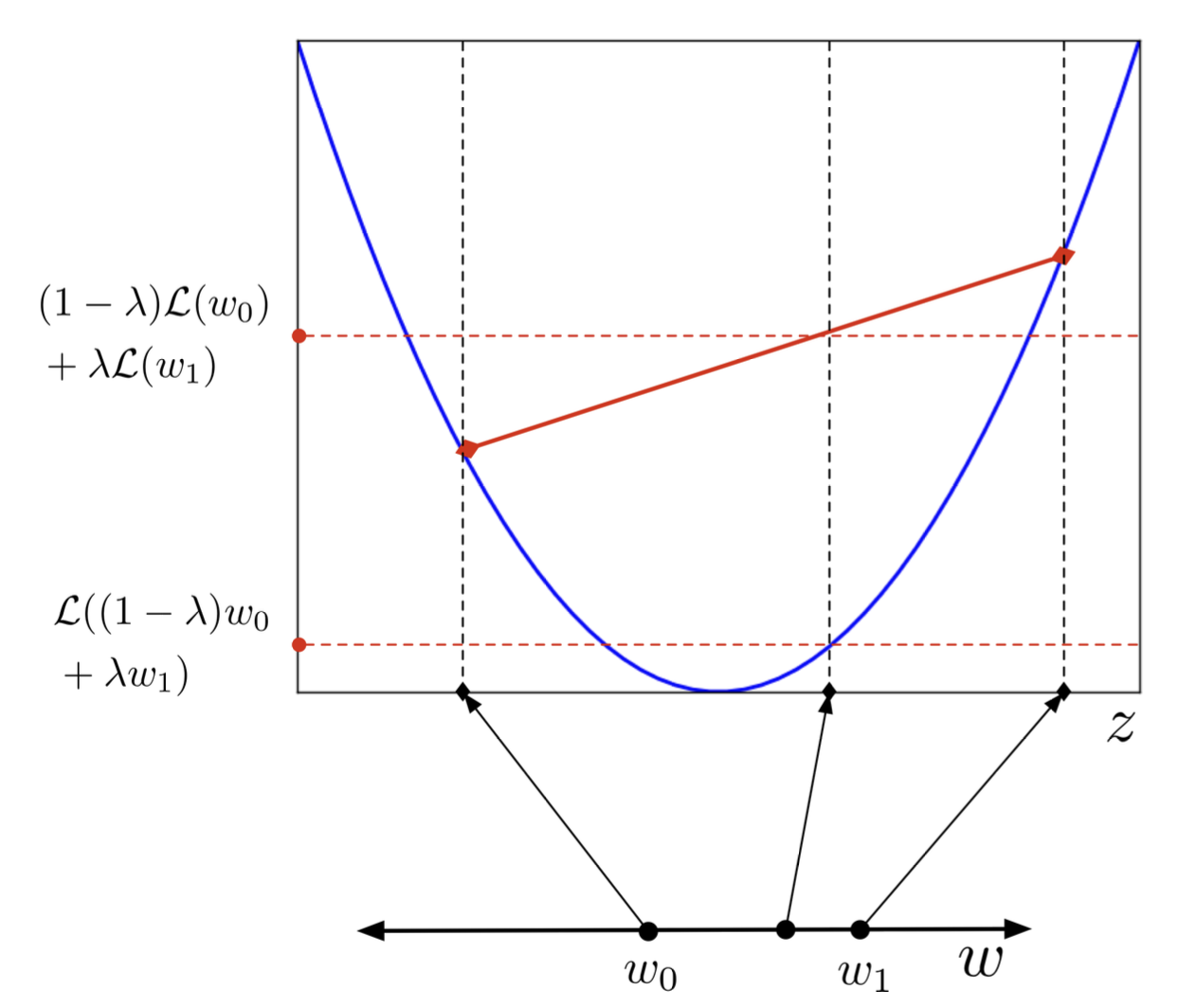
Convex Functions is bowl-shaped, 다시 말해 아래로 볼록한 함수를 convex라고 한다. 위로 볼록한 경우는 concave라고 부른다.
convex function의 특징으로 위 그래프를 관찰하면 \(w_{0},w_{1}\)의 함수 값의 내분점이 x좌표의 내분점의 함수값보다 크다는 것이 직관적으로 보인다. Concave는 부등호가 반대로 적용된다.
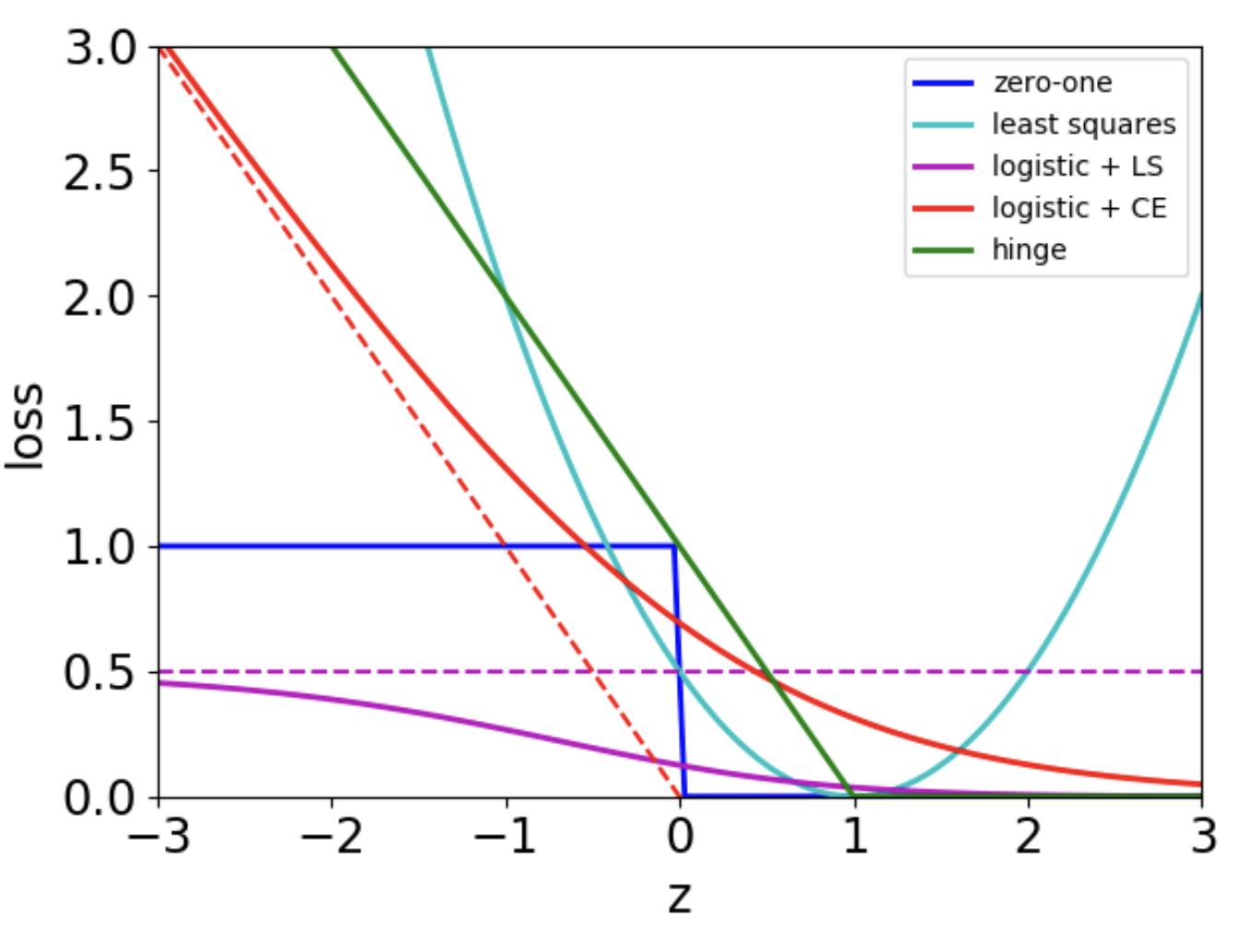
위 loss function 종류중에 convex인것은 무엇일까?
- Hinge, least squares, logistic + CE 이 convex에 해당한다.
- logisitc + LS는 안되는걸까? 0을 중심으로 오른쪽은 아래로 볼록이지만 왼쪽은 위로 볼록이기 때문에 Convex도 Concave도 아니다.
- zero-one 는 안되는 반례가 존재한다. (e.g. \(w_{0}=-1,w_{1}=1\), 1:2내분점을 구하면 Convex 등식이 성립하지 않는다.)
Summary
Why we talk about convex?
- All critical points are minimia
- Gradient descent find optimal solution
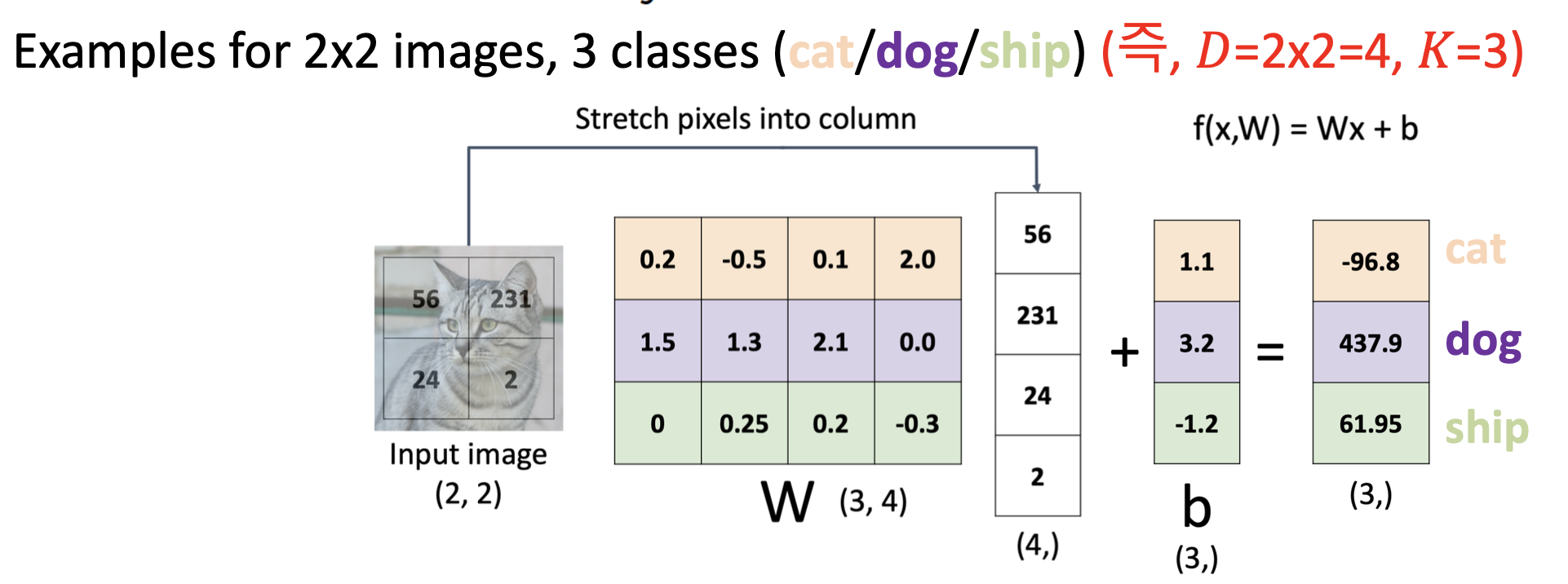
Multiclass classification
- Targets form a discrete set \(\left\{ 1,\cdots,K \right\}\
- Represent one-hot vectors, or a one-of-K encoding
- If entry K is 1, then \(t=\{ 0,\cdots,1,\cdots,0 \} \)
- D inputs vectors K output vectors \(\Rightarrow\) KXD weight matrix \(w\), also K-dimension bias vector \(b\)
Softmax function
- a multivariable generalization of the logistic function
\(y_{K}=softmax(z_{1},\cdots,z_{K})_{k}=\frac{e^{z_{K}}}{\sum_{k'}e^{z_{K}}}\)
(The input \(z_{k}\) are called the logits)
Properties :
- Outputs are positive and sum to 1 (probabailities of each class)
- The largest probability than th others is selected the prediction class (soft-argmax)
- Softmax with K=2 \(\Rightarrow\) logisitic function
Cross Entropy equation for multivariable label
\(L_{CE}(y,t)=-\sum_{k=1}{K}t_{k}log(y_{k})=-t^{T}(log(y))\)
(t : one-hot vector)
Typically combine the softmax and cross-entropy into a softmax-cross-entropy function
\(z=Wx+b\)
\(y=softmax(z)\)
\(L_{CE}=-t^{T}(log(y))\)
\(\frac{\partial L_{CE}}{\partial z}=y-t\)
Why? Check this proof [link]
'Machine Learning' 카테고리의 다른 글
| How many data need for ML model? (0) | 2023.02.28 |
|---|---|
| What is SVMs? (2) | 2022.12.20 |
| What is Linear Classification? [Ⅰ] (0) | 2022.12.17 |
| What is Linear Regression? (0) | 2022.10.12 |



