ROKO
What is SVMs? 본문
Binary classification
Targets : \(t \in \{ -1,+1 \} \)
Linear model : \(z=w^{T}x+b, y=sign(z)\)
Loss function : \(L_{0-1}=\mathbb{I} \{ y \neq t \} \)

Hyperplane에 두 종류의 데이터가 표시되어있다. 이 두 종류의 데이터를 분류하기 위한 linear classifier로 위와같은 모델을 선택 할 수 있다.

하지만 가능한 모델은 하나일까? 아니라면 어떤 모델이 최선일까?
Optimal Separating Hyperplane
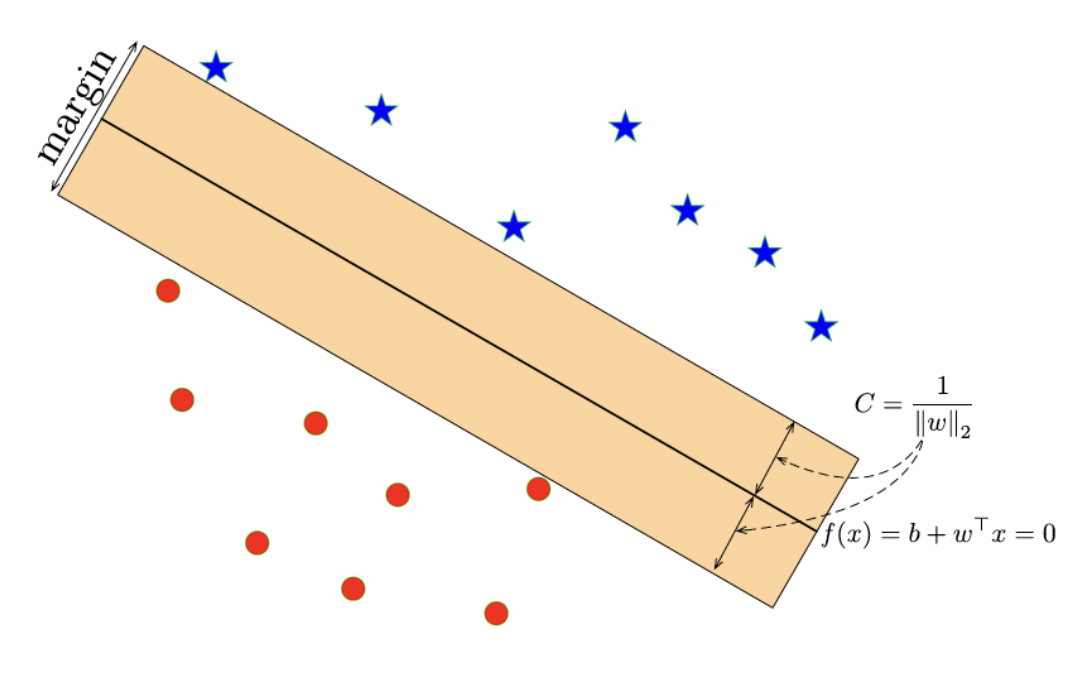
직관적으로 보면 각 데이터를 분류하면서도 margin이 최대로 되어있는 linear classifier가 가장 적합하다. margin이 최대라는 뜻은 generalization이 가장 잘 되어있다고 생각 할 수도 있다.
이제 Optimal한 경우를 얻기 위해서는 margin을 정의해야 한다. margin을 정의하기 위한 수식을 살펴보자.

임의의 두 점 \(x_{1}\)와 \(x_{2}\)은 \(f(x)\) 위에 있다.
\(w^{T}x_{1}+b=0, w^{T}X_{2}+b=0\)
\(Difference : w^{T}(x_{2}-x_{1}))=0\)
It means w is orthogonal to hyperplane since \(x_{1},x_{2}\) are arbitrary points on the hyperplane.
\(w^{*}\) is unit vector \(\frac{w}{||w||_{2}}\) in the same direction as \(w\), \(||w||_{2}\) means L2-norm of \(w\).
Let \(x_{proj}=x'+\alpha w^{*}\), \(x'\) is also a point on the hyperplane.
\(w^{T}x_{proj}+b=0\) holds.
If we can get \(\alpha\) value, then \(| \alpha |\) is a distance from x' to hyperplane. (why? \(||w^{*}|| = 1\), orthogonal to hyperplane)
\(w^{T}(x'+\alpha w^{*})+b=0\)
\(w^{T}(x'+\alpha \frac{w}{||w||_{2}})+b=0\)
\(w^{T}x'+\alpha \frac{w^{T}w}{||w||_{2}}+b=0\)
\(w^{T}x'+\alpha \frac{||w||_{2}^{2}}{||w||_{2}}+b=0\)
\(w^{T}x'+\alpha ||w||_{2}+b=0\)
\(\alpha = \frac{w^{T}x'+b}{||w||_{2}} \Rightarrow\) The signed distance of a point x' to the hyperplane.
Recall :
\(sign(w^Tx+b)=t^{(i)}\)
\(t^{(i)}(w^Tx+b)>0\) Why? They are not zero and same sign.
\(t^{(i)} \frac{(w^Tx+b)}{||w||_{2}} \geq | \alpha| (=C)\) Combine with signed distance.
margin을 수식으로 정의하였으므로 이제 최적화 목적함수를 만들 수 있다.
Max-margin objective : \(\underset{w,b}{max} \; C \; s.t. t^{(i)} \frac{(w^Tx+b)}{||w||_{2}} \geq C \; i=1,\cdots,N \)
Let \(C=\frac{1}{||w||_2}\) to simplify
\(t^{(i)} \frac{(w^Tx+b)}{||w||_{2}} \geq \frac{1}{||w||_2} \Leftrightarrow t^{(i)}(w^T+b) \geq 1\)
Change aspect from Geometric margin constraint to Algebraic margin constraint
Equivalent optimization objective : \(min \; ||w||^2_2 \; s.t. \; t^{(i)}(w^T+b) \geq 1 \; i=1,\cdots,N \)
만약 margin에 포함되는 data가 있다면 training set에서 제외하여 부등식을 만족시킬 수 있다.
이는 separating hyperplane을 결정하는 중요 변수가 margin 영역 안에 있는 data들이라는 뜻으로 해석할 수도 있다. 그리고 그러한 data 값들을 support vectors라고 부른다.
따라서 위의 알고리즘은 (hard) Support-Vector Machine (SVM)이라고 불린다.
SVM-like algorithms(max-margin, large-margin)

linearly separable하지 않은 데이터 분포를 SVM-like algorithm을 이용해 분류하려면 어떤 과정이 필요할까?

misclassified된 값들을 일부 허용한다. 허용되는 수치는 slack variables \(\xi_i\)로 표현하고 total amount of slack을 penalize(constraint)한다.
Soft margin constraint : \(\underset{w,b,\xi}{min} \; \frac{1}{2}||w||^2_2+\gamma\sum^N_{i=1}\xi_i \; s.t. \;\frac{t^{(i)}(w^Tx^{(i)}+b)}{||w||_2} \geq C(1-\xi_i), for \; \xi_i \geq 0 \; i=1,\cdots,N \)
- \(\gamma\) is a hyperparameter that trades off the margin with the amount of slack.
- \(\gamma = 0\), \(w,b=0,\xi = 1\)이 되어 부등식을 만족
- \(\gamma \rightarrow \infty \), hard-margin objective
- \(\sum_i \xi_i\)를 penalize해도 같은 결과를 도출해낼 수 있다.
Simplify the soft margin constraint
\( t^{(i)}(w^Tx^{(i)}+b) \geq 1-\xi_i \; i=1,\cdots,N \)
\( \xi_i \geq 1-t^{(i)}(w^Tx^{(i)}+b) \)
\(case1 \; : \; 1-t^{(i)}(w^Tx^{(i)}+b) \leq 0 \Rightarrow \xi_i=0\)
\(case2 \; : \; 1-t^{(i)}(w^Tx^{(i)}+b) > 0 \Rightarrow \xi_i=1-t^{(i)}(w^Tx^{(i)}+b)\)
\(\xi_i = max\{ 0, 1-t^{(i)}(w^Tx^{(i)}+b) \} \Rightarrow Hinge \; Loss\)
\(\sum_{(i=1)}^N \xi_i = \sum_{(i=1)}^N max\{ 0, 1-t^{(i)}(w^Tx^{(i)}+b) \} \)
\(\underset{w,b,\xi}{min} \sum^N_{(i=1)} max\{ 0, 1-t^{(i)}y^{(i)}(w,b) \} + \frac{1}{2\gamma} ||w||^2_2 \)
- The loss function \(L_H(y,t)=max\{ 0,1-ty \} \) is called the hinge loss
- Second term is the \(L_2 norm\) of the weights
- soft-margin SVM is a linear classifier with hinge loss and an \(L_2\) regularizer
Then how to fit W?
- gradient descent
- reformulate with the Lagrange dual
'Artificial Intelligence > Machine Learning' 카테고리의 다른 글
| Is validation necessary? (0) | 2023.02.28 |
|---|---|
| How many data need for ML model? (0) | 2023.02.28 |
| What is Linear Classification? [Ⅱ] (0) | 2022.12.19 |
| What is Linear Classification? [Ⅰ] (0) | 2022.12.17 |



