ROKO
Generative models 본문
Discriminative models : P(Y|X)을 바로 추정하는 확률모델
Generative models : P(X|Y)를 추정하는 확률 모델

생성모델의 의미
X가 어떤 class인지 확률을 아는 것보다 class를 대표하는 데이터는 어떠한 형태일까를 추정하는게 더 좋지 않을까?
Bayes Classifier
\(h(x)=\underset{k}{argmax}p(t=k|x)\)
\(=\underset{k}{argmax}\frac{p(x|t=k)p(t=k)}{p(x)}\)
\(=\underset{k}{argmax}p(x|t=k)p(t=k)\)
What if x is discrete or continous?
x 변수가 이산형 분포인지 연속형 분포인지에 따라 생각해보자는 의미이다.
이산형일 경우 이산개의 확률로 나타내면 그만이고 연속형일 경우 연속인 범위를 나타내는 가우시안분포와 같은 확률분포를 사용해야 한다.
What if x is multivariate?
- Multiple measurements
- Nxd matrix (N instances, d features)
- Mutivariate Parameters
- Mean : \(E[x]=[\mu_1,\cdots,\mu_d]^T\)
- Covariance : \(\Sigma=Cov(x)=E[(x-\mu)^T(x-\mu)] \rightarrow\) dxd covariance matrix
Multivariate Gaussian Distribution
\(p(x)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}exp[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)]\)
다변수 가우시안 분포를 이용해 생성모델을 구성할텐데 이전에 다변수 가우시안 분포부터 알아보자.
Mahalanobis distance : \((x-\mu_k)^T\Sigma^{-1}(x-\mu_k)\), 분산을 고려한 평균부터 x까지의 거리
이는 서로 다른 분산과 상관관계를 고려하여 거리를 구할 수 있게 해준다.

Gaussian Discriminant Anaylsis (GDA, GBC, Gaussian Bayes Classfier)
GDA는 p(X|t)를 다변수 정규분폴로 추정하는 가우시안 베이즈 분류기이다.
각 다변수 가우시안은 평균과 공분산으로 표현할 수 있다.
따라서 필요한 모든 파라미터는 \(O(d^2)~mean(d)+covariance(d^2)\)이다.
공분산을 모두 추정하는건 많은 연산량을 요구한다.
GBC의 결정경계는 class의 posterior에 결정된다.
다시말해서 각 class의 score가 같은 경계를 다 모으면 결정경계가 되는 것이다.
\(Score \; logp(t_k|x)=logp(x|t_k)+logp(t_k)-logp(x)\)
\(=-\frac{d}{2}log(2\pi)-\frac{1}{2}log|\Sigma^{-1}_k|-\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)+logp(t_k)-logp(x)\)
Decision boundary:
where class k score = class l score \(\rightarrow\) Quadratic function in x
\((x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)=(x-\mu_l)^T\Sigma^{-1}_l(x-\mu_k)+Const\)
\(x^T\Sigma^{-1}_kx-2\mu_k^T\Sigma_k^{-1}x-2\mu_l^T\Sigma_l^{-1}x+Const\)

데이터의 class가 많아질수록 구해야하는 분포의 parameters들이 많아져 연산과 시간복잡도의 부담이 생긴다. 트릭이나 가정을 사용해 매개변수 추정 시간을 줄여야 한다. "서로 다른 class끼리 같은(공유) 분산을 가지고 있다는 가정"을 이용하면 추정해야할 매개변수가 상당히 많이 줄어든다.
Let's assume that \(\Sigma_k=\Sigma_l\)
In MLE, 결정경계 = 선형결정경계(Linear decision boundary)
\(-2\mu_k^T\Sigma_k^{-1}x=-2\mu^T_l\Sigma_l^{-1}x+Const\)
class간의 분산 공유를 가정으로한 방법을 LDA(Linear Discriminant Analysis)라고 부르기도 한다.
이진분류 문제에 대해서 GDA를 수식화하면 Logistic Regression과 같은 식이 나오는 신기한 현상을 볼 수 있다.
\(p(t|x,\Pi,\mu_0,\mu_1,\Sigma)=\frac{1}{1+exp(-w^Tx)}\)
그렇다면 우린 GDA와 LR중 어떤 것을 선택해야 할까? (식이 같다고 모델도 같지 않다는것 주의)
- GDA는 class를 기반으로 강한 추정을 하고 점진적으로 더 효율적이다. (다변수 가우시안)
- LR은 GDA보다 더 강인하며, 이상치에 덜 민감하다.
- Why? GDA는 이상치를 포함하여 확률 분포를 추정하고 결정경계를 결정한다면 LR은 loss식에 이상치가 있다라더라도 sigmoid를 통해 덜 민감하게 반영되기 때문에 강인하다고 볼 수 있다
- 많은 class-conditional distribution은 logistic classifier를 따른다.
- 가우시안 분포가 아닌 경우 LR은 GDA와 비견한 성능을 지닌다.
- GDA는 missing value를 다루기 쉽다.
아직 공분산의 추정 매개변수는 \(d^2\)로 데이터 feature dimension에 따라 qudraticgkrp 증가한다.
이때 navie bayes를 적용해보자. 각 feature 변수들이 독립이라고 기정하는것이다. 그러면 평균 d개 분산 d개(diagnoal matrix) 총 2d개의 parameter만 찾으면 된다.
Decision Boundatry: isotorpic
\(logp(t_k|x)=-\frac{1}{2\sigma^2}(x-\mu_k)^T(x-\mu_k)\)
\(=-\frac{1}{2\sigma^2}||x-\mu_k||^2\)
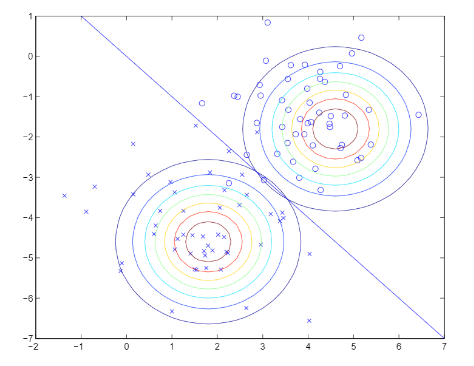
결정경계가 각 분포의 평균에 상당히 많은 영향을 받는것을 알 수 있다. 공분산의 경우 독립이라는 나이브 베이즈 가정에 의해 영향이 줄어들고 분산의 크기만 영향을 끼칠수 밖에 없는 것이다.
Summary
- GDA - quadratic decision boundary
- GDA with shared covariance is same equation to LR
- Generative models
- flexible, easy to add\remove class
- handle missing data naturally
혹여 Genrative와 Discriminative의 차이를 잘 모르겠는분들은 해당 블로그를 참조하시면 수식적으로 이해가 쉬울것이라고 생각된다.
https://medium.com/@mlengineer/generative-and-discriminative-models-af5637a66a3
Generative VS Discriminative Models
I would like to start this write up with a story.
medium.com
https://fabiandablander.com/statistics/Two-Properties.html
Two properties of the Gaussian distribution
In a previous blog post, we looked at the history of least squares, how Gauss justified it using the Gaussian distribution, and how Laplace justified the Gaussian distribution using the central limit theorem. The Gaussian distribution has a number of speci
fabiandablander.com
https://learnopencv.com/generative-and-discriminative-models/
Generative and Discriminative Models | LearnOpenCV #
Most of the Machine Learning and Deep Learning problems that you solve are conceptualized from the Generative and Discriminative Models. In Machine Learning, one can clearly distinguish between the two modelling types: Classifying an image as a dog or a ca
learnopencv.com
'Machine Learning' 카테고리의 다른 글
| GMM (Gaussian Mixture Model) (0) | 2023.03.18 |
|---|---|
| K-Means (0) | 2023.03.16 |
| Probabilistic models [Ⅱ] (0) | 2023.03.15 |
| Probabilistic Models [Ⅰ] (4) | 2023.03.12 |




