ROKO
What is Data Structure? 본문
Data Structure
- a set of data & a set of operations on the data
- This is a structure that makes easy to access and to use data
- Appropriate DT(data structure) makes more faster and more efficient program, but inappropriate DT make performance worse !
General Data Structure
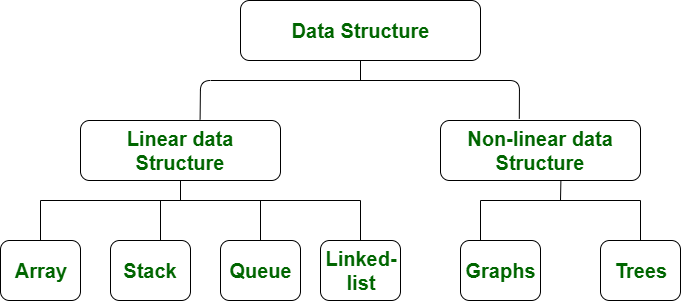
Program = Data Structure(how easy to treat data) + Algorithm(how easy to solve problem)
So be a good programmer, we should select proper method both
Then how to measure efficiency and cost?
- Time Complexity (e.g. Wall-clock time)
- Space Complexity (e.g. memory usage)
There is no the most efficient data structure -> Check Trade-off between DT's pros and cons
Select DT case by case
Abstract Data Type (ADT)
- Mathematical definition of data type
- a set of objects and a set of operations
e.g. integer's ADT
- a set of objects : {..., -1, 0, 1, ...}
- a set of operations : {+, -, X, %, >, ...}
Purpose of ADT : Seperate specification and implementation
- Specification : what is a data type, operations
- Implementation : how to implement ?
e.g.
- Objects : 1 ~ INT_MAX
- Operations : add(x,y) -> return x+y
ADT
- Logical form : abstract def of data (e.g. interger)
- Phsical form : implemtation of data (e.g. 32bits)

How to know Time & Space Costs
Empirical method
Time : Wall-clock time, measure the real time
start_time = tic
Run an algorithm
end_time = toc
run_time = tic - tocSpace : memory usage (VmPeak)
cat /proc/$pid/statuspros : easy, intuitive
cons : variable for HW, OS, PL, etc(need several experiment), do not know exactly when input size increases to infinity
Theoretical method
complexity analysis
- \(T(n)\) : time complexity for given \(n\) input data
- \(S(n)\) : space complexity for given \(n\) input data
Time complexity
- Basic operations are constant time C
- Add, Substraction, Assignment, Comparison
# A
sum = 0
for i in range(0,n):
sum = sum + n
# B
sum = 0
for i in range(0, n):
for j in range(0, n):
sum =sum + 1
# C
sum = n * n| Algorithm A | Algorithm B | Algorithm C | |
| Assignments | n + 1 | n x n + 1 | 1 |
| Additions | n | n x n | |
| Multiplications | 1 | ||
| Total | \(2n + 1\) | \(2n^2+1\) | \(2\) |
we can know Algorithm C is the most efficient
Time complexity divided to Best, Average, Worst case
Must consider Wrost case !! Why? To gaurantee minimum performance
Asymptotic Analysis
Find time complexity when input n increases to inifinity
- Big - 0 (\(O\),Upper bound) Notation
- Big - 0mega (\(\Omega\),Lower bound) Notation
- Big - Theta (\(\Theta\),Exact bound) Notation
Definition \(T(n) = O(f(n)) [n \to \infty]\)
\(T(n)\; is\; the\; set\; O(f(n)) \)
\( if\; there\; exist\; two\; positive\; constants\; c\; and\; n_0 \)
\( s \cdot t\; T(n) \leq cf(n)\; for\; all\; n \geq n_0\)

Big-O notation can be strict and loose
e.g. \(T(n) = 3n^2 = \{ O(n^2), O(n^3), O(n^4), \cdots \} \)
If someone says " assume Big-O tightly " -> \(T(n) = O(n^2)\)
Several Big-O notation

'Data Structrue' 카테고리의 다른 글
| List (리스트) (0) | 2023.01.15 |
|---|---|
| Deque (덱) (0) | 2023.01.14 |
| Queue (큐) (0) | 2023.01.12 |
| Stack (스택) (0) | 2023.01.11 |




