ROKO
[coursera] Neural Networks and Deep Learning: Week 2-1 본문
[coursera] Neural Networks and Deep Learning: Week 2-1
RO_KO 2024. 6. 29. 01:48
고양이 사진을 입력으로 받아 고양이인지 아닌지 이진분류하는 로지스틱 회귀 모델에 대해 얘기한다.

우선 컬러 색상이 있는 이미지의 경우 이미지의 높이, 너비와 색을 표현하기 위한 R,G,B 3가지 채널로 분리되어 총 HxWx3의 숫자들로 표현된 데이터로 나타낼 수 있다.
따라서 모델의 목표는 HxWx3 의 크기에 해당하는 데이터를 input으로 받아 고양이가 맞다면 1 아니라면 0을 반환하는 과정을 학습하는 것이 목표다.
표기 정의
- \((x,y) \, x \in R^{n_x},y \in \{ 0,1\} \) - \( n_x \): feature 크기, x: data, y: label
- \( m: \{ (x^{(1)}, y^{(1)}) \cdots (x^{(m)}, y^{(m)}) \} \) - 학습데이터 개수
- \( X: R^{n_x \times m } \) - 학습데이터 배치 행렬
- \( Y: R^{1 \times m} \) - 정답데이터 행렬
이러한 표기 정의는 신경망을 설계하는 과정에서 복잡성을 줄여준다.
Logistic Regression
주어진 \( x \in R^{n_x} \)에 대해서 \( \hat{y}=P(y=1|x) \) 확률을 계산하기를 원한다.
간단하게 가중치 (parameters) : \( w \in R^{n_x}, b \in R \)을 이용해 output \( = \hat{y}=w^Tx+b \)를 계산 할 수 있다.

하지만 이는 0과 1사이의 확률값이 아닌 상수가 나오므로 output에 시그모이드 함수 \( \sigma = \frac{1}{1+e^{-z}} \) 를 이용해 0과 1사이의 확률로 scaling 해줄 수 있다. (간단한 설명으로 표현하는것 같으나 로지스틱 회귀의 등장배경은 더 이론적인 근거가 있다.)
What is Linear Classification? [Ⅰ]
Classification : Predicting a discrete-valued target Binary class (pos / neg, 0/1, true/false) Multiclass Binary linear classification linear model \(z = w^{T}x + b \) \(y=\left\{\begin{matrix} 1 \; if \; z \geq r\\ 0 \; if \; z < r \end{matrix}\right.\) w
ro-ko.tistory.com
따라서 output \( = \sigma(\hat{y}=w^Tx+b) \) 로 표현할 수 있다.
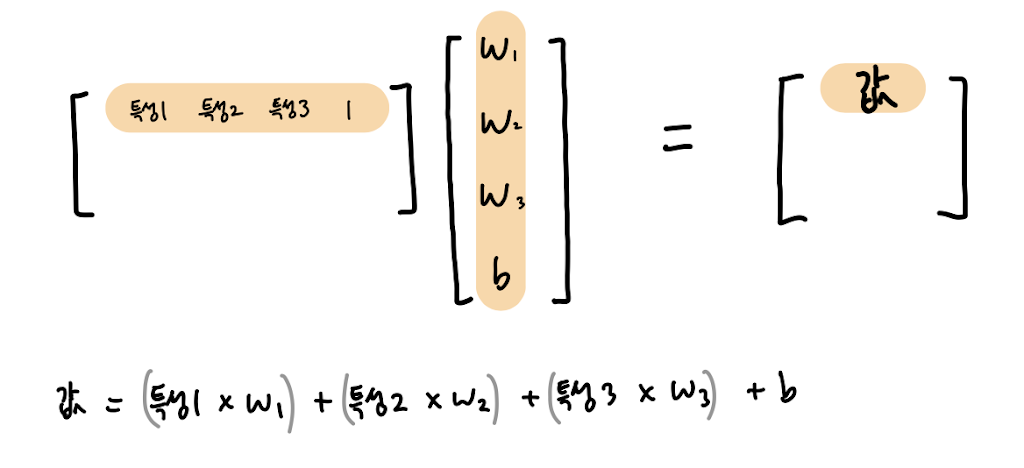
이때 간단한 트릭을 소개하는데 x feature 값에 \( x_0 = 1 \)을 추가해 가중치 행렬과 편향 (bias)를 합쳐 하나의 행렬 연산으로 변형 할 수 있다.
output \( =\sigma(\theta x), \hat{y}=\theta x \)로 표현되며 이는 코드를 최적화와 병렬 연산 능력을 활용하는 좋은 방식이다.
Cost function
\( \hat{y}=\sigma()w^T x+b), \sigma (z)= \frac{1}{1+e^{-z}}, z^{(i)}=w^T x^{(i)}+b \)
주어진 모든 데이터 \( \{ (x^{(1)}, y^{(1)}) \cdots (x^{(m)}, y^{(m)}) \} \) 에서 모델이 얼마나 잘 예측하는지 각 데이터마다 \( \hat{y}^{(i)} \approx y^{(i)} \) 비교하여 점수를 계산해야한다.
cost function: \(J(w,b)=\frac{1}{m}\sum_{i=1}^m L(\hat{y}^{(i)}, y^{(i)})\)
이는 학습 데이터가 i.i.d(independent and identically distributed) 이라는 가정하에 maximum likelihood estimation을 통해 cost 함수를 모델링한 것을 의미한다.
Loss (error) function
각 데이터마다 loss를 계산할 수 있다. 단순하게 \( L(\hat{y}, y)=\frac{1}{2}(\hat{y}-y)^2 \)를 사용할 수도 있지만 적절한 함수가 아니다. 왜냐하면 convex함수가 아니기 때문에 미분이 0이 되는 지점을 찾아도 global minimum이 아닌 local minimum일수도 있기 때문이다.
하지만 loss function 을 \( L(\hat{y}, y)=-y\log{\hat{y}}+(1-y)\log(1-\hat{y}) \) (binary cross entropy)로 사용하게 된다면 convex 가 만족한다.
자세한 설명으로 관련 글 링크를 확인해보자.
Using Mean squared error loss (MSE) in Logistic Regression?
I have been revisiting some algorithms/concepts that were on the verge of vanishing from my memory :) while revising the logistic…
medium.com
선형 행렬은 convex라 하더라도 sigmoid가 convex, concave도 아닌 함수이기 때문에 둘의 합성함수는 convex가 아니다.
https://www.quora.com/Is-the-composition-of-two-convex-functions-also-convex
Is the composition of two convex functions also convex?
Answer (1 of 4): Short Answer: No. A bit longer answer: There is one more condition that needs to be checked for claiming the convexity of the composition. Let f(x) = h(g(x)); then it is convex when: 1. h is convex and non-decreasing, and g is convex; 2. h
www.quora.com
logisitic regression (cross entropy) 가 convex인 이유는 아래 링크에 있다.
Logistic regression - Prove That the Cost Function Is Convex
I'm reading about Hole House (HoleHouse) - Stanford Machine Learning Notes - Logistic Regression. You can do a find on "convex" to see the part that relates to my question. Background: $h_\theta(...
math.stackexchange.com
* loss 함수는 데이터 하나, cost는 모든 입력 데이터에 대한 비용계산 이라는 차이를 기억하자.
Convex
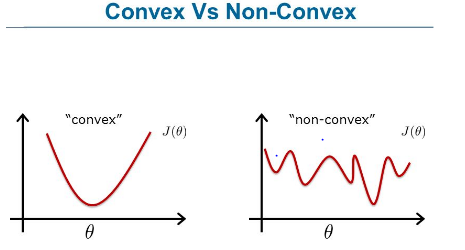
convex 상태를 중요시 여기는 이유는 모델이 convex하다면 어느 위치에서 가중치를 초기화하더라도 경사하강법을 이용해 global minimum값에 수렴할 수 밖에 없기 때문이다.
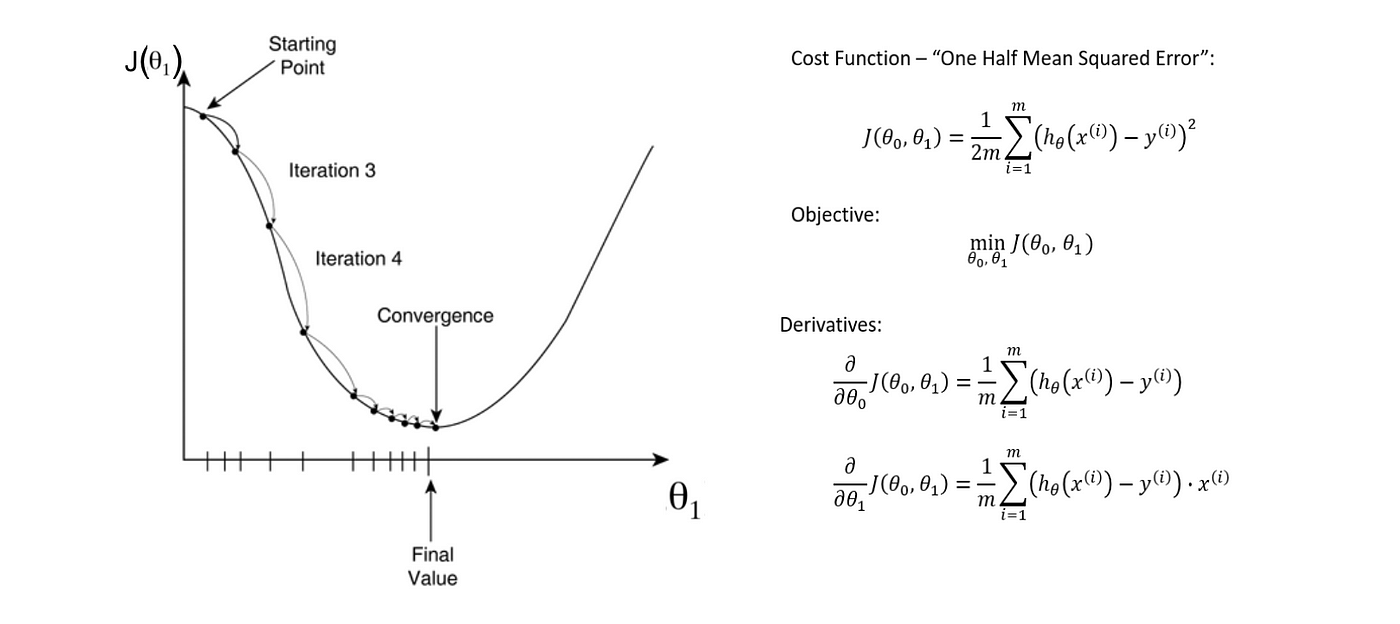
- \(w:= w-\alpha\frac{dJ(w,b)}{dw}\), \(\alpha\): learning rate
- \(b:= b-\alpha\frac{dJ(w,b)}{db} \)
가중치를 모델의 gradient를 통해 업데이트하면 어떻게 수렴하는지 위 그림과 함께 파악해보자. learning rate의 경우는 값이 클수록 더 빠르게 수렴하지만 부정확한 단점이 있고 작을수록 정확하지만 느리게 수렴하는 단점이 있다.
Computational graph
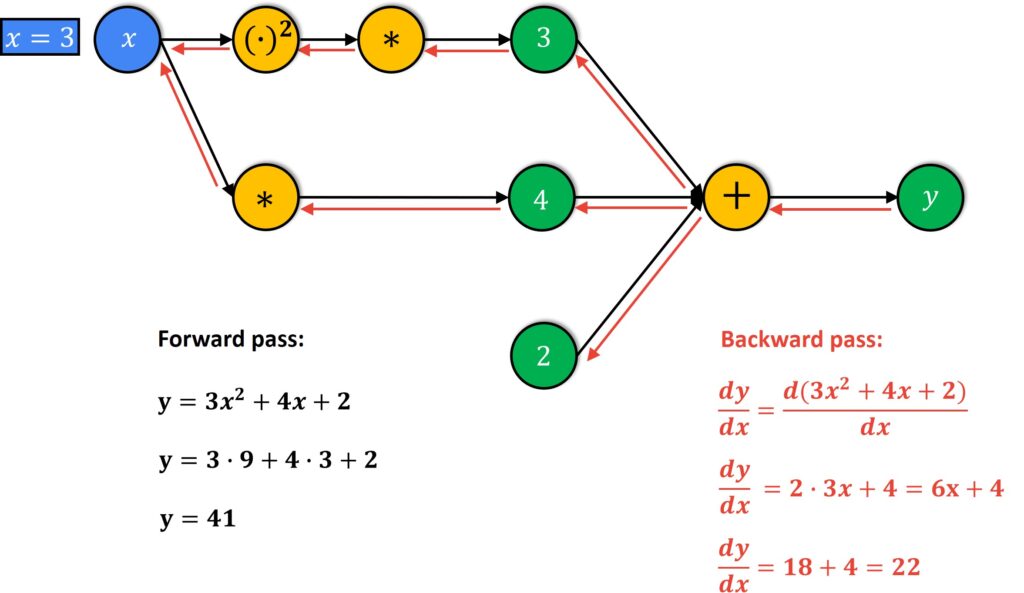
신경망은 순전파 (forward propagation)와 역전파 (backward propagation)의 단계로 진행된다.
left-to-right 연산을 forward, right-to-left 연산을 backward로 보면 된다. 예시 그림은 각 연산을 하나의 노드로 표현한 computational graph이다.
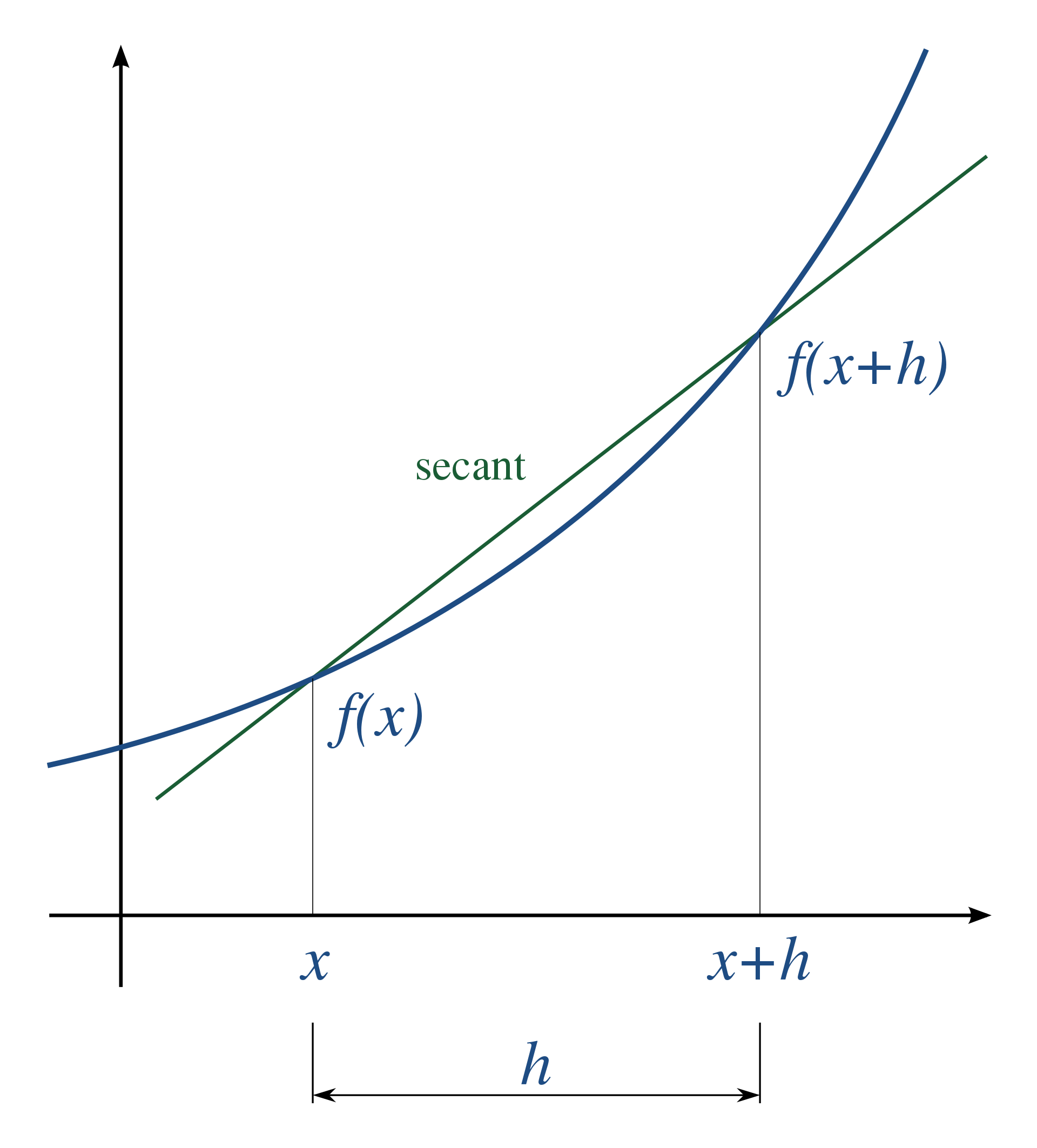
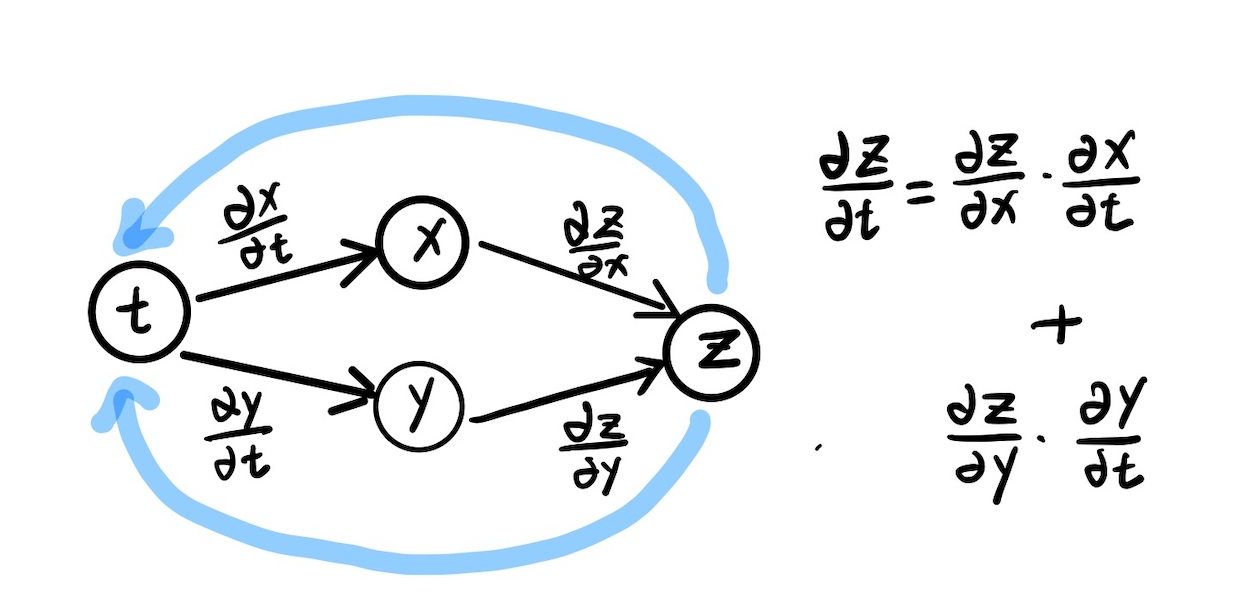
왼쪽과 같이 numeric derivatives는 error propagation의 우려와 많은 연산량을 요구한다. 하지만 오른쪽의 chain rule을 이용하면 정확하고 빠르게 계산이 가능하다.
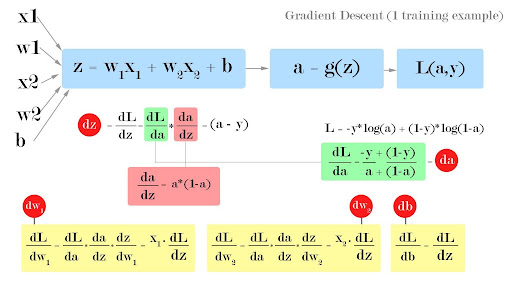
Notation
- \(w_i\): accumulator로 쓰였기 때문에 superscript가 없음
- \(z^{(i)}\): 각 training data 하나당 결과이기 때문에 superscript가 있음
logistic regression을 위해선 2 loop가 필요
- forward
- backward
data가 많아질수록 for loop 연산이 많아지고 이는 코드 비효율적으로 실행되게 된다. 이를 위해서 vectorization을 활용하여 병렬 연산을 통해 최적화 한다.
'Artificial Intelligence > Deep Learning' 카테고리의 다른 글
| [coursera] Neural Networks and Deep Learning: Week 3 (0) | 2024.06.29 |
|---|---|
| [coursera] Neural Networks and Deep Learning: Week 2-2 (0) | 2024.06.29 |
| [coursera] Neural Networks and Deep Learning: Week 1 (0) | 2024.06.28 |
| AE (Autoencoder) (0) | 2023.03.07 |




